Chapter 20 Week15_1: Lavaan Lab 17 Second-order and Bifactor Models
In this lab, we will evaluate the dimensionality of ISMI-29 by fitting and comparing the following four models:
- Unidimensional model (one-factor CFA)
- Correlated factors model (multi-factor CFA)
- Second-order factor model
- Bifactor model
Load up the lavaan and semPlot libraries:
library(lavaan)
library(semPlot)- In this lab, we will work with the ISMI-29 data that are collected using Internalized Stigma of Mental Illness Scale
- 758 participants and 29 items
- Let’s read in the dataset:
ISMI29 = read.csv('ISMI-29 n758 (Hammer 16).csv', header = F)Take a look at the dataset:
head(ISMI29)## V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14 V15 V16 V17 V18 V19
## 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 2 2 1 2
## 2 4 4 4 3 4 4 2 2 1 1 2 2 3 2 2 3 3 2 3
## 3 4 4 3 1 1 1 2 1 2 1 3 2 1 3 3 3 3 3 3
## 4 1 1 2 1 1 3 2 1 1 1 1 1 1 3 2 1 1 1 2
## 5 3 3 4 1 1 3 3 2 2 1 1 1 1 2 1 1 1 1 1
## 6 2 2 3 2 2 3 2 1 2 1 1 1 1 1 1 1 1 1 3
## V20 V21 V22 V23 V24 V25 V26 V27 V28 V29
## 1 1 2 1 1 2 1 1 2 2 2
## 2 3 2 2 4 2 2 4 4 1 2
## 3 3 3 1 3 2 2 4 3 1 2
## 4 1 3 1 2 1 1 1 1 1 2
## 5 2 1 1 1 1 2 3 1 2 2
## 6 2 2 2 4 1 2 3 1 1 3sample size:
n <- nrow(ISMI29)
n #758## [1] 758Factor structure:
- Item1-6: Alienation “Having a mental illness has spoiled my life.”
- Item7-13: Stereotype Endorsement “Mentally ill people tend to be violent”
- Item14-18: Discrimination Experience “People discriminate against me because I have a mental illness”
- Item19-24: Social Withdrawal “I don’t talk about myself as much because I don’t want to burden others with my mental illness”
- Item25-29: *Stigma Resistance (*reverse-coded) “I can have a good, fulfilling life, despite my mental illness”
20.1 PART I: Unidimensional model
Write out syntax for a one-factor CFA model:
uni.model = '
ISMI =~ V1+V2+V3+V4+V5+V6+V7+V8+V9+V10+V11+V12+V13+V14+V15+V16+V17+V18+V19+
V20+V21+V22+V23+V24+V25+V26+V27+V28+V29
'Fit the model:
- It is recommended to fix the variances of all first- and second-order factors to be 1 (lavaan: std.lv = TRUE) and request standardized solutions;
uni.model.fit = lavaan::sem(uni.model,
data=ISMI29,
ordered = colnames(ISMI29),
std.lv = TRUE,
fixed.x = F)
summary(uni.model.fit, standardized = TRUE, fit.measures = TRUE)## lavaan 0.6-12 ended normally after 15 iterations
##
## Estimator DWLS
## Optimization method NLMINB
## Number of model parameters 116
##
## Number of observations 758
##
## Model Test User Model:
## Standard Robust
## Test Statistic 2140.966 2606.734
## Degrees of freedom 377 377
## P-value (Chi-square) 0.000 0.000
## Scaling correction factor 0.869
## Shift parameter 143.934
## simple second-order correction
##
## Model Test Baseline Model:
##
## Test statistic 76016.286 21485.170
## Degrees of freedom 406 406
## P-value 0.000 0.000
## Scaling correction factor 3.587
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.977 0.894
## Tucker-Lewis Index (TLI) 0.975 0.886
##
## Robust Comparative Fit Index (CFI) NA
## Robust Tucker-Lewis Index (TLI) NA
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.079 0.088
## 90 Percent confidence interval - lower 0.075 0.085
## 90 Percent confidence interval - upper 0.082 0.092
## P-value RMSEA <= 0.05 0.000 0.000
##
## Robust RMSEA NA
## 90 Percent confidence interval - lower NA
## 90 Percent confidence interval - upper NA
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.073 0.073
##
## Parameter Estimates:
##
## Standard errors Robust.sem
## Information Expected
## Information saturated (h1) model Unstructured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv
## ISMI =~
## V1 0.788 0.016 50.143 0.000 0.788
## V2 0.730 0.018 40.532 0.000 0.730
## V3 0.523 0.027 19.276 0.000 0.523
## V4 0.699 0.019 36.908 0.000 0.699
## V5 0.693 0.020 33.790 0.000 0.693
## V6 0.726 0.018 40.699 0.000 0.726
## V7 0.556 0.027 20.637 0.000 0.556
## V8 0.586 0.032 18.105 0.000 0.586
## V9 0.306 0.038 7.953 0.000 0.306
## V10 0.678 0.026 26.009 0.000 0.678
## V11 0.661 0.025 26.609 0.000 0.661
## V12 0.572 0.034 16.904 0.000 0.572
## V13 0.758 0.023 32.495 0.000 0.758
## V14 0.660 0.022 29.922 0.000 0.660
## V15 0.654 0.023 28.747 0.000 0.654
## V16 0.738 0.018 40.911 0.000 0.738
## V17 0.707 0.020 35.246 0.000 0.707
## V18 0.764 0.017 44.135 0.000 0.764
## V19 0.583 0.025 23.420 0.000 0.583
## V20 0.768 0.016 46.920 0.000 0.768
## V21 0.773 0.017 46.637 0.000 0.773
## V22 0.744 0.018 40.995 0.000 0.744
## V23 0.710 0.020 35.129 0.000 0.710
## V24 0.739 0.019 39.098 0.000 0.739
## V25 0.071 0.038 1.893 0.058 0.071
## V26 0.728 0.019 37.856 0.000 0.728
## V27 0.665 0.024 27.941 0.000 0.665
## V28 0.359 0.038 9.485 0.000 0.359
## V29 0.213 0.035 5.994 0.000 0.213
## Std.all
##
## 0.788
## 0.730
## 0.523
## 0.699
## 0.693
## 0.726
## 0.556
## 0.586
## 0.306
## 0.678
## 0.661
## 0.572
## 0.758
## 0.660
## 0.654
## 0.738
## 0.707
## 0.764
## 0.583
## 0.768
## 0.773
## 0.744
## 0.710
## 0.739
## 0.071
## 0.728
## 0.665
## 0.359
## 0.213
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv
## .V1 0.000 0.000
## .V2 0.000 0.000
## .V3 0.000 0.000
## .V4 0.000 0.000
## .V5 0.000 0.000
## .V6 0.000 0.000
## .V7 0.000 0.000
## .V8 0.000 0.000
## .V9 0.000 0.000
## .V10 0.000 0.000
## .V11 0.000 0.000
## .V12 0.000 0.000
## .V13 0.000 0.000
## .V14 0.000 0.000
## .V15 0.000 0.000
## .V16 0.000 0.000
## .V17 0.000 0.000
## .V18 0.000 0.000
## .V19 0.000 0.000
## .V20 0.000 0.000
## .V21 0.000 0.000
## .V22 0.000 0.000
## .V23 0.000 0.000
## .V24 0.000 0.000
## .V25 0.000 0.000
## .V26 0.000 0.000
## .V27 0.000 0.000
## .V28 0.000 0.000
## .V29 0.000 0.000
## ISMI 0.000 0.000
## Std.all
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
##
## Thresholds:
## Estimate Std.Err z-value P(>|z|) Std.lv
## V1|t1 -0.980 0.054 -17.991 0.000 -0.980
## V1|t2 -0.099 0.046 -2.178 0.029 -0.099
## V1|t3 1.046 0.056 18.722 0.000 1.046
## V2|t1 -0.903 0.053 -17.036 0.000 -0.903
## V2|t2 0.213 0.046 4.643 0.000 0.213
## V2|t3 1.202 0.060 20.103 0.000 1.202
## V3|t1 -1.149 0.058 -19.687 0.000 -1.149
## V3|t2 -0.070 0.046 -1.524 0.127 -0.070
## V3|t3 1.175 0.059 19.899 0.000 1.175
## V4|t1 -0.985 0.055 -18.053 0.000 -0.985
## V4|t2 -0.066 0.046 -1.452 0.147 -0.066
## V4|t3 1.058 0.056 18.840 0.000 1.058
## V5|t1 -0.785 0.051 -15.374 0.000 -0.785
## V5|t2 -0.046 0.046 -1.016 0.309 -0.046
## V5|t3 1.029 0.056 18.542 0.000 1.029
## V6|t1 -0.758 0.051 -14.965 0.000 -0.758
## V6|t2 0.060 0.046 1.307 0.191 0.060
## V6|t3 1.202 0.060 20.103 0.000 1.202
## V7|t1 -0.685 0.050 -13.793 0.000 -0.685
## V7|t2 0.537 0.048 11.189 0.000 0.537
## V7|t3 1.711 0.080 21.292 0.000 1.711
## V8|t1 0.404 0.047 8.614 0.000 0.404
## V8|t2 1.606 0.075 21.452 0.000 1.606
## V8|t3 2.183 0.118 18.488 0.000 2.183
## V9|t1 0.264 0.046 5.729 0.000 0.264
## V9|t2 1.711 0.080 21.292 0.000 1.711
## V9|t3 2.656 0.194 13.656 0.000 2.656
## V10|t1 0.261 0.046 5.656 0.000 0.261
## V10|t2 1.429 0.067 21.257 0.000 1.429
## V10|t3 2.149 0.114 18.786 0.000 2.149
## V11|t1 0.073 0.046 1.597 0.110 0.073
## V11|t2 1.319 0.063 20.826 0.000 1.319
## V11|t3 2.261 0.127 17.776 0.000 2.261
## V12|t1 0.507 0.048 10.619 0.000 0.507
## V12|t2 1.839 0.088 20.845 0.000 1.839
## V12|t3 2.413 0.148 16.268 0.000 2.413
## V13|t1 0.288 0.046 6.235 0.000 0.288
## V13|t2 1.438 0.068 21.282 0.000 1.438
## V13|t3 2.031 0.103 19.706 0.000 2.031
## V14|t1 -0.632 0.049 -12.885 0.000 -0.632
## V14|t2 0.496 0.048 10.405 0.000 0.496
## V14|t3 1.476 0.069 21.369 0.000 1.476
## V15|t1 -0.401 0.047 -8.542 0.000 -0.401
## V15|t2 0.771 0.051 15.170 0.000 0.771
## V15|t3 1.726 0.081 21.255 0.000 1.726
## V16|t1 -0.557 0.048 -11.544 0.000 -0.557
## V16|t2 0.534 0.048 11.118 0.000 0.534
## V16|t3 1.549 0.072 21.455 0.000 1.549
## V17|t1 -0.285 0.046 -6.162 0.000 -0.285
## V17|t2 0.803 0.051 15.644 0.000 0.803
## V17|t3 1.771 0.084 21.114 0.000 1.771
## V18|t1 -0.437 0.047 -9.260 0.000 -0.437
## V18|t2 0.632 0.049 12.885 0.000 0.632
## V18|t3 1.726 0.081 21.255 0.000 1.726
## V19|t1 -1.243 0.061 -20.393 0.000 -1.243
## V19|t2 -0.210 0.046 -4.570 0.000 -0.210
## V19|t3 0.888 0.053 16.840 0.000 0.888
## V20|t1 -0.664 0.049 -13.445 0.000 -0.664
## V20|t2 0.278 0.046 6.018 0.000 0.278
## V20|t3 1.251 0.061 20.439 0.000 1.251
## V21|t1 -0.727 0.050 -14.485 0.000 -0.727
## V21|t2 0.433 0.047 9.189 0.000 0.433
## V21|t3 1.517 0.071 21.429 0.000 1.517
## V22|t1 -0.261 0.046 -5.656 0.000 -0.261
## V22|t2 0.758 0.051 14.965 0.000 0.758
## V22|t3 1.656 0.077 21.400 0.000 1.656
## V23|t1 -0.572 0.048 -11.827 0.000 -0.572
## V23|t2 0.440 0.047 9.332 0.000 0.440
## V23|t3 1.447 0.068 21.306 0.000 1.447
## V24|t1 -0.323 0.046 -6.957 0.000 -0.323
## V24|t2 0.789 0.051 15.441 0.000 0.789
## V24|t3 1.571 0.073 21.461 0.000 1.571
## V25|t1 -0.873 0.052 -16.644 0.000 -0.873
## V25|t2 0.437 0.047 9.260 0.000 0.437
## V25|t3 1.420 0.067 21.231 0.000 1.420
## V26|t1 -1.001 0.055 -18.238 0.000 -1.001
## V26|t2 0.306 0.046 6.596 0.000 0.306
## V26|t3 1.236 0.061 20.346 0.000 1.236
## V27|t1 -0.481 0.048 -10.120 0.000 -0.481
## V27|t2 0.854 0.052 16.380 0.000 0.854
## V27|t3 1.683 0.079 21.354 0.000 1.683
## V28|t1 0.254 0.046 5.512 0.000 0.254
## V28|t2 1.656 0.077 21.400 0.000 1.656
## V28|t3 1.982 0.099 20.046 0.000 1.982
## V29|t1 -0.698 0.050 -14.001 0.000 -0.698
## V29|t2 0.619 0.049 12.674 0.000 0.619
## V29|t3 1.756 0.083 21.166 0.000 1.756
## Std.all
## -0.980
## -0.099
## 1.046
## -0.903
## 0.213
## 1.202
## -1.149
## -0.070
## 1.175
## -0.985
## -0.066
## 1.058
## -0.785
## -0.046
## 1.029
## -0.758
## 0.060
## 1.202
## -0.685
## 0.537
## 1.711
## 0.404
## 1.606
## 2.183
## 0.264
## 1.711
## 2.656
## 0.261
## 1.429
## 2.149
## 0.073
## 1.319
## 2.261
## 0.507
## 1.839
## 2.413
## 0.288
## 1.438
## 2.031
## -0.632
## 0.496
## 1.476
## -0.401
## 0.771
## 1.726
## -0.557
## 0.534
## 1.549
## -0.285
## 0.803
## 1.771
## -0.437
## 0.632
## 1.726
## -1.243
## -0.210
## 0.888
## -0.664
## 0.278
## 1.251
## -0.727
## 0.433
## 1.517
## -0.261
## 0.758
## 1.656
## -0.572
## 0.440
## 1.447
## -0.323
## 0.789
## 1.571
## -0.873
## 0.437
## 1.420
## -1.001
## 0.306
## 1.236
## -0.481
## 0.854
## 1.683
## 0.254
## 1.656
## 1.982
## -0.698
## 0.619
## 1.756
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv
## .V1 0.379 0.379
## .V2 0.467 0.467
## .V3 0.727 0.727
## .V4 0.511 0.511
## .V5 0.520 0.520
## .V6 0.473 0.473
## .V7 0.691 0.691
## .V8 0.656 0.656
## .V9 0.907 0.907
## .V10 0.541 0.541
## .V11 0.563 0.563
## .V12 0.672 0.672
## .V13 0.425 0.425
## .V14 0.564 0.564
## .V15 0.573 0.573
## .V16 0.455 0.455
## .V17 0.500 0.500
## .V18 0.416 0.416
## .V19 0.660 0.660
## .V20 0.410 0.410
## .V21 0.402 0.402
## .V22 0.447 0.447
## .V23 0.495 0.495
## .V24 0.453 0.453
## .V25 0.995 0.995
## .V26 0.470 0.470
## .V27 0.558 0.558
## .V28 0.871 0.871
## .V29 0.955 0.955
## ISMI 1.000 1.000
## Std.all
## 0.379
## 0.467
## 0.727
## 0.511
## 0.520
## 0.473
## 0.691
## 0.656
## 0.907
## 0.541
## 0.563
## 0.672
## 0.425
## 0.564
## 0.573
## 0.455
## 0.500
## 0.416
## 0.660
## 0.410
## 0.402
## 0.447
## 0.495
## 0.453
## 0.995
## 0.470
## 0.558
## 0.871
## 0.955
## 1.000
##
## Scales y*:
## Estimate Std.Err z-value P(>|z|) Std.lv
## V1 1.000 1.000
## V2 1.000 1.000
## V3 1.000 1.000
## V4 1.000 1.000
## V5 1.000 1.000
## V6 1.000 1.000
## V7 1.000 1.000
## V8 1.000 1.000
## V9 1.000 1.000
## V10 1.000 1.000
## V11 1.000 1.000
## V12 1.000 1.000
## V13 1.000 1.000
## V14 1.000 1.000
## V15 1.000 1.000
## V16 1.000 1.000
## V17 1.000 1.000
## V18 1.000 1.000
## V19 1.000 1.000
## V20 1.000 1.000
## V21 1.000 1.000
## V22 1.000 1.000
## V23 1.000 1.000
## V24 1.000 1.000
## V25 1.000 1.000
## V26 1.000 1.000
## V27 1.000 1.000
## V28 1.000 1.000
## V29 1.000 1.000
## Std.all
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000Plot the path diagram:
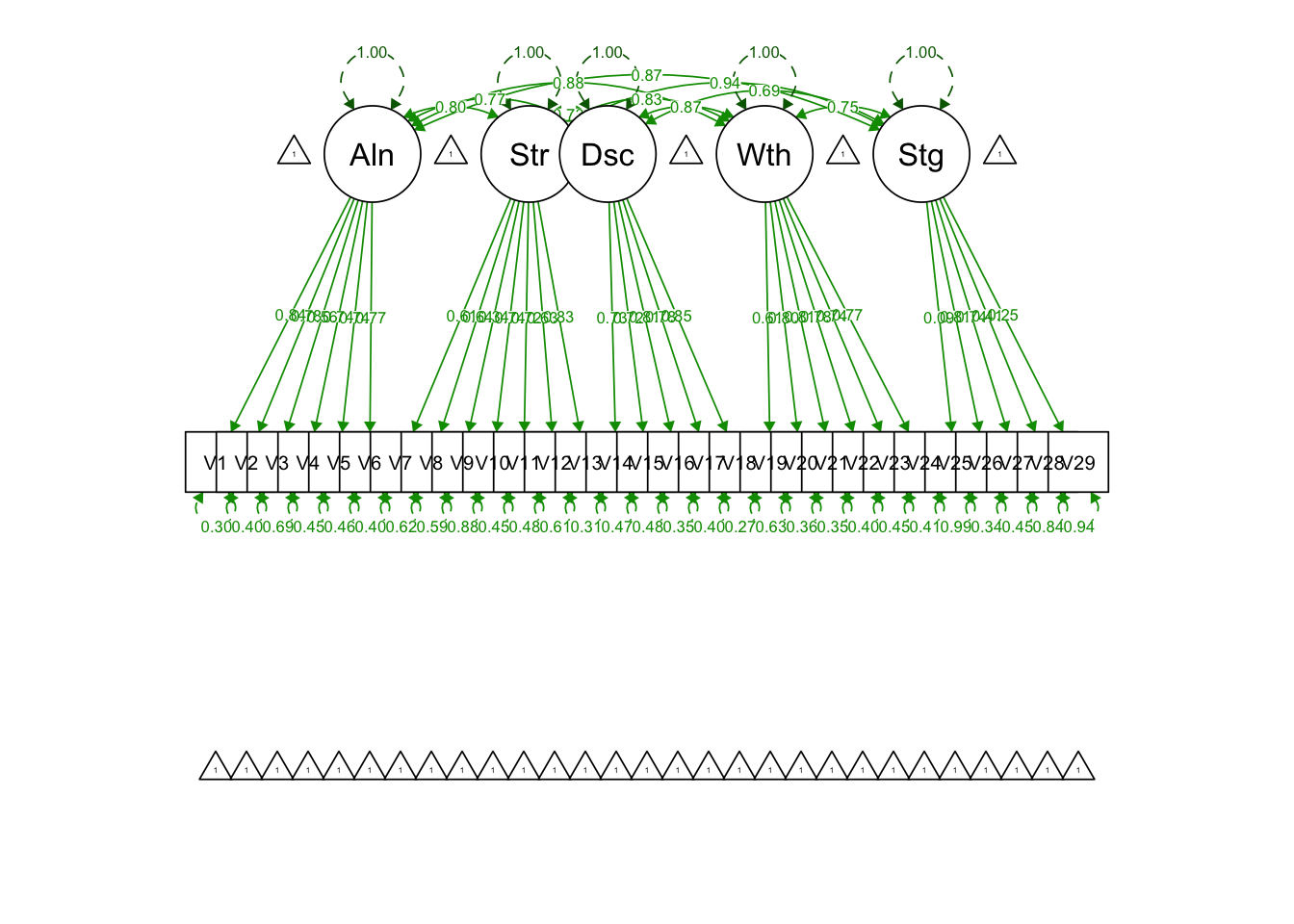
semPaths(uni.model.fit, what = 'std', fade = F)
20.2 PART II: Correlated factors model
Write out syntax for a five-factor CFA model:
cor.fac.model = '
Alienation =~ V1+V2+V3+V4+V5+V6
Stereotype =~ V7+V8+V9+V10+V11+V12+V13
Discrimination =~ V14+V15+V16+V17+V18
Withdrawal =~ V19+V20+V21+V22+V23+V24
Stigma =~ V25+V26+V27+V28+V29
'cor.fac.model.fit = lavaan::sem(cor.fac.model,
data=ISMI29,
ordered = colnames(ISMI29),
std.lv = TRUE,
fixed.x = F)
summary(cor.fac.model.fit, standardized = TRUE, fit.measures = TRUE)## lavaan 0.6-12 ended normally after 43 iterations
##
## Estimator DWLS
## Optimization method NLMINB
## Number of model parameters 126
##
## Number of observations 758
##
## Model Test User Model:
## Standard Robust
## Test Statistic 1340.188 1751.387
## Degrees of freedom 367 367
## P-value (Chi-square) 0.000 0.000
## Scaling correction factor 0.829
## Shift parameter 133.939
## simple second-order correction
##
## Model Test Baseline Model:
##
## Test statistic 76016.286 21485.170
## Degrees of freedom 406 406
## P-value 0.000 0.000
## Scaling correction factor 3.587
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.987 0.934
## Tucker-Lewis Index (TLI) 0.986 0.927
##
## Robust Comparative Fit Index (CFI) NA
## Robust Tucker-Lewis Index (TLI) NA
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.059 0.071
## 90 Percent confidence interval - lower 0.056 0.067
## 90 Percent confidence interval - upper 0.063 0.074
## P-value RMSEA <= 0.05 0.000 0.000
##
## Robust RMSEA NA
## 90 Percent confidence interval - lower NA
## 90 Percent confidence interval - upper NA
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.059 0.059
##
## Parameter Estimates:
##
## Standard errors Robust.sem
## Information Expected
## Information saturated (h1) model Unstructured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv
## Alienation =~
## V1 0.839 0.016 52.254 0.000 0.839
## V2 0.776 0.018 42.466 0.000 0.776
## V3 0.556 0.028 19.804 0.000 0.556
## V4 0.743 0.019 39.776 0.000 0.743
## V5 0.735 0.020 36.553 0.000 0.735
## V6 0.773 0.018 43.805 0.000 0.773
## Stereotype =~
## V7 0.614 0.028 21.657 0.000 0.614
## V8 0.643 0.034 19.107 0.000 0.643
## V9 0.342 0.041 8.341 0.000 0.342
## V10 0.741 0.026 28.172 0.000 0.741
## V11 0.724 0.025 29.166 0.000 0.724
## V12 0.627 0.035 18.158 0.000 0.627
## V13 0.830 0.023 36.031 0.000 0.830
## Discrimination =~
## V14 0.727 0.021 34.282 0.000 0.727
## V15 0.720 0.022 32.614 0.000 0.720
## V16 0.809 0.016 50.107 0.000 0.809
## V17 0.776 0.019 41.474 0.000 0.776
## V18 0.853 0.019 45.026 0.000 0.853
## Withdrawal =~
## V19 0.609 0.026 23.873 0.000 0.609
## V20 0.801 0.016 50.440 0.000 0.801
## V21 0.808 0.017 48.511 0.000 0.808
## V22 0.776 0.018 43.680 0.000 0.776
## V23 0.743 0.021 36.183 0.000 0.743
## V24 0.771 0.019 40.946 0.000 0.771
## Stigma =~
## V25 0.090 0.042 2.159 0.031 0.090
## V26 0.814 0.020 40.736 0.000 0.814
## V27 0.739 0.024 30.998 0.000 0.739
## V28 0.406 0.040 10.062 0.000 0.406
## V29 0.249 0.038 6.479 0.000 0.249
## Std.all
##
## 0.839
## 0.776
## 0.556
## 0.743
## 0.735
## 0.773
##
## 0.614
## 0.643
## 0.342
## 0.741
## 0.724
## 0.627
## 0.830
##
## 0.727
## 0.720
## 0.809
## 0.776
## 0.853
##
## 0.609
## 0.801
## 0.808
## 0.776
## 0.743
## 0.771
##
## 0.090
## 0.814
## 0.739
## 0.406
## 0.249
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv
## Alienation ~~
## Stereotype 0.798 0.021 37.898 0.000 0.798
## Discrimination 0.767 0.019 41.097 0.000 0.767
## Withdrawal 0.876 0.014 60.655 0.000 0.876
## Stigma 0.868 0.019 46.044 0.000 0.868
## Stereotype ~~
## Discrimination 0.731 0.023 31.608 0.000 0.731
## Withdrawal 0.825 0.019 44.132 0.000 0.825
## Stigma 0.937 0.017 53.800 0.000 0.937
## Discrimination ~~
## Withdrawal 0.868 0.014 62.437 0.000 0.868
## Stigma 0.688 0.028 24.773 0.000 0.688
## Withdrawal ~~
## Stigma 0.755 0.024 31.564 0.000 0.755
## Std.all
##
## 0.798
## 0.767
## 0.876
## 0.868
##
## 0.731
## 0.825
## 0.937
##
## 0.868
## 0.688
##
## 0.755
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv
## .V1 0.000 0.000
## .V2 0.000 0.000
## .V3 0.000 0.000
## .V4 0.000 0.000
## .V5 0.000 0.000
## .V6 0.000 0.000
## .V7 0.000 0.000
## .V8 0.000 0.000
## .V9 0.000 0.000
## .V10 0.000 0.000
## .V11 0.000 0.000
## .V12 0.000 0.000
## .V13 0.000 0.000
## .V14 0.000 0.000
## .V15 0.000 0.000
## .V16 0.000 0.000
## .V17 0.000 0.000
## .V18 0.000 0.000
## .V19 0.000 0.000
## .V20 0.000 0.000
## .V21 0.000 0.000
## .V22 0.000 0.000
## .V23 0.000 0.000
## .V24 0.000 0.000
## .V25 0.000 0.000
## .V26 0.000 0.000
## .V27 0.000 0.000
## .V28 0.000 0.000
## .V29 0.000 0.000
## Alienation 0.000 0.000
## Stereotype 0.000 0.000
## Discrimination 0.000 0.000
## Withdrawal 0.000 0.000
## Stigma 0.000 0.000
## Std.all
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
##
## Thresholds:
## Estimate Std.Err z-value P(>|z|) Std.lv
## V1|t1 -0.980 0.054 -17.991 0.000 -0.980
## V1|t2 -0.099 0.046 -2.178 0.029 -0.099
## V1|t3 1.046 0.056 18.722 0.000 1.046
## V2|t1 -0.903 0.053 -17.036 0.000 -0.903
## V2|t2 0.213 0.046 4.643 0.000 0.213
## V2|t3 1.202 0.060 20.103 0.000 1.202
## V3|t1 -1.149 0.058 -19.687 0.000 -1.149
## V3|t2 -0.070 0.046 -1.524 0.127 -0.070
## V3|t3 1.175 0.059 19.899 0.000 1.175
## V4|t1 -0.985 0.055 -18.053 0.000 -0.985
## V4|t2 -0.066 0.046 -1.452 0.147 -0.066
## V4|t3 1.058 0.056 18.840 0.000 1.058
## V5|t1 -0.785 0.051 -15.374 0.000 -0.785
## V5|t2 -0.046 0.046 -1.016 0.309 -0.046
## V5|t3 1.029 0.056 18.542 0.000 1.029
## V6|t1 -0.758 0.051 -14.965 0.000 -0.758
## V6|t2 0.060 0.046 1.307 0.191 0.060
## V6|t3 1.202 0.060 20.103 0.000 1.202
## V7|t1 -0.685 0.050 -13.793 0.000 -0.685
## V7|t2 0.537 0.048 11.189 0.000 0.537
## V7|t3 1.711 0.080 21.292 0.000 1.711
## V8|t1 0.404 0.047 8.614 0.000 0.404
## V8|t2 1.606 0.075 21.452 0.000 1.606
## V8|t3 2.183 0.118 18.488 0.000 2.183
## V9|t1 0.264 0.046 5.729 0.000 0.264
## V9|t2 1.711 0.080 21.292 0.000 1.711
## V9|t3 2.656 0.194 13.656 0.000 2.656
## V10|t1 0.261 0.046 5.656 0.000 0.261
## V10|t2 1.429 0.067 21.257 0.000 1.429
## V10|t3 2.149 0.114 18.786 0.000 2.149
## V11|t1 0.073 0.046 1.597 0.110 0.073
## V11|t2 1.319 0.063 20.826 0.000 1.319
## V11|t3 2.261 0.127 17.776 0.000 2.261
## V12|t1 0.507 0.048 10.619 0.000 0.507
## V12|t2 1.839 0.088 20.845 0.000 1.839
## V12|t3 2.413 0.148 16.268 0.000 2.413
## V13|t1 0.288 0.046 6.235 0.000 0.288
## V13|t2 1.438 0.068 21.282 0.000 1.438
## V13|t3 2.031 0.103 19.706 0.000 2.031
## V14|t1 -0.632 0.049 -12.885 0.000 -0.632
## V14|t2 0.496 0.048 10.405 0.000 0.496
## V14|t3 1.476 0.069 21.369 0.000 1.476
## V15|t1 -0.401 0.047 -8.542 0.000 -0.401
## V15|t2 0.771 0.051 15.170 0.000 0.771
## V15|t3 1.726 0.081 21.255 0.000 1.726
## V16|t1 -0.557 0.048 -11.544 0.000 -0.557
## V16|t2 0.534 0.048 11.118 0.000 0.534
## V16|t3 1.549 0.072 21.455 0.000 1.549
## V17|t1 -0.285 0.046 -6.162 0.000 -0.285
## V17|t2 0.803 0.051 15.644 0.000 0.803
## V17|t3 1.771 0.084 21.114 0.000 1.771
## V18|t1 -0.437 0.047 -9.260 0.000 -0.437
## V18|t2 0.632 0.049 12.885 0.000 0.632
## V18|t3 1.726 0.081 21.255 0.000 1.726
## V19|t1 -1.243 0.061 -20.393 0.000 -1.243
## V19|t2 -0.210 0.046 -4.570 0.000 -0.210
## V19|t3 0.888 0.053 16.840 0.000 0.888
## V20|t1 -0.664 0.049 -13.445 0.000 -0.664
## V20|t2 0.278 0.046 6.018 0.000 0.278
## V20|t3 1.251 0.061 20.439 0.000 1.251
## V21|t1 -0.727 0.050 -14.485 0.000 -0.727
## V21|t2 0.433 0.047 9.189 0.000 0.433
## V21|t3 1.517 0.071 21.429 0.000 1.517
## V22|t1 -0.261 0.046 -5.656 0.000 -0.261
## V22|t2 0.758 0.051 14.965 0.000 0.758
## V22|t3 1.656 0.077 21.400 0.000 1.656
## V23|t1 -0.572 0.048 -11.827 0.000 -0.572
## V23|t2 0.440 0.047 9.332 0.000 0.440
## V23|t3 1.447 0.068 21.306 0.000 1.447
## V24|t1 -0.323 0.046 -6.957 0.000 -0.323
## V24|t2 0.789 0.051 15.441 0.000 0.789
## V24|t3 1.571 0.073 21.461 0.000 1.571
## V25|t1 -0.873 0.052 -16.644 0.000 -0.873
## V25|t2 0.437 0.047 9.260 0.000 0.437
## V25|t3 1.420 0.067 21.231 0.000 1.420
## V26|t1 -1.001 0.055 -18.238 0.000 -1.001
## V26|t2 0.306 0.046 6.596 0.000 0.306
## V26|t3 1.236 0.061 20.346 0.000 1.236
## V27|t1 -0.481 0.048 -10.120 0.000 -0.481
## V27|t2 0.854 0.052 16.380 0.000 0.854
## V27|t3 1.683 0.079 21.354 0.000 1.683
## V28|t1 0.254 0.046 5.512 0.000 0.254
## V28|t2 1.656 0.077 21.400 0.000 1.656
## V28|t3 1.982 0.099 20.046 0.000 1.982
## V29|t1 -0.698 0.050 -14.001 0.000 -0.698
## V29|t2 0.619 0.049 12.674 0.000 0.619
## V29|t3 1.756 0.083 21.166 0.000 1.756
## Std.all
## -0.980
## -0.099
## 1.046
## -0.903
## 0.213
## 1.202
## -1.149
## -0.070
## 1.175
## -0.985
## -0.066
## 1.058
## -0.785
## -0.046
## 1.029
## -0.758
## 0.060
## 1.202
## -0.685
## 0.537
## 1.711
## 0.404
## 1.606
## 2.183
## 0.264
## 1.711
## 2.656
## 0.261
## 1.429
## 2.149
## 0.073
## 1.319
## 2.261
## 0.507
## 1.839
## 2.413
## 0.288
## 1.438
## 2.031
## -0.632
## 0.496
## 1.476
## -0.401
## 0.771
## 1.726
## -0.557
## 0.534
## 1.549
## -0.285
## 0.803
## 1.771
## -0.437
## 0.632
## 1.726
## -1.243
## -0.210
## 0.888
## -0.664
## 0.278
## 1.251
## -0.727
## 0.433
## 1.517
## -0.261
## 0.758
## 1.656
## -0.572
## 0.440
## 1.447
## -0.323
## 0.789
## 1.571
## -0.873
## 0.437
## 1.420
## -1.001
## 0.306
## 1.236
## -0.481
## 0.854
## 1.683
## 0.254
## 1.656
## 1.982
## -0.698
## 0.619
## 1.756
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv
## .V1 0.297 0.297
## .V2 0.398 0.398
## .V3 0.690 0.690
## .V4 0.449 0.449
## .V5 0.460 0.460
## .V6 0.403 0.403
## .V7 0.623 0.623
## .V8 0.586 0.586
## .V9 0.883 0.883
## .V10 0.451 0.451
## .V11 0.476 0.476
## .V12 0.607 0.607
## .V13 0.311 0.311
## .V14 0.471 0.471
## .V15 0.481 0.481
## .V16 0.346 0.346
## .V17 0.398 0.398
## .V18 0.272 0.272
## .V19 0.629 0.629
## .V20 0.359 0.359
## .V21 0.347 0.347
## .V22 0.398 0.398
## .V23 0.448 0.448
## .V24 0.405 0.405
## .V25 0.992 0.992
## .V26 0.337 0.337
## .V27 0.454 0.454
## .V28 0.835 0.835
## .V29 0.938 0.938
## Alienation 1.000 1.000
## Stereotype 1.000 1.000
## Discrimination 1.000 1.000
## Withdrawal 1.000 1.000
## Stigma 1.000 1.000
## Std.all
## 0.297
## 0.398
## 0.690
## 0.449
## 0.460
## 0.403
## 0.623
## 0.586
## 0.883
## 0.451
## 0.476
## 0.607
## 0.311
## 0.471
## 0.481
## 0.346
## 0.398
## 0.272
## 0.629
## 0.359
## 0.347
## 0.398
## 0.448
## 0.405
## 0.992
## 0.337
## 0.454
## 0.835
## 0.938
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
##
## Scales y*:
## Estimate Std.Err z-value P(>|z|) Std.lv
## V1 1.000 1.000
## V2 1.000 1.000
## V3 1.000 1.000
## V4 1.000 1.000
## V5 1.000 1.000
## V6 1.000 1.000
## V7 1.000 1.000
## V8 1.000 1.000
## V9 1.000 1.000
## V10 1.000 1.000
## V11 1.000 1.000
## V12 1.000 1.000
## V13 1.000 1.000
## V14 1.000 1.000
## V15 1.000 1.000
## V16 1.000 1.000
## V17 1.000 1.000
## V18 1.000 1.000
## V19 1.000 1.000
## V20 1.000 1.000
## V21 1.000 1.000
## V22 1.000 1.000
## V23 1.000 1.000
## V24 1.000 1.000
## V25 1.000 1.000
## V26 1.000 1.000
## V27 1.000 1.000
## V28 1.000 1.000
## V29 1.000 1.000
## Std.all
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000semPaths(cor.fac.model.fit, what = 'std', fade = F)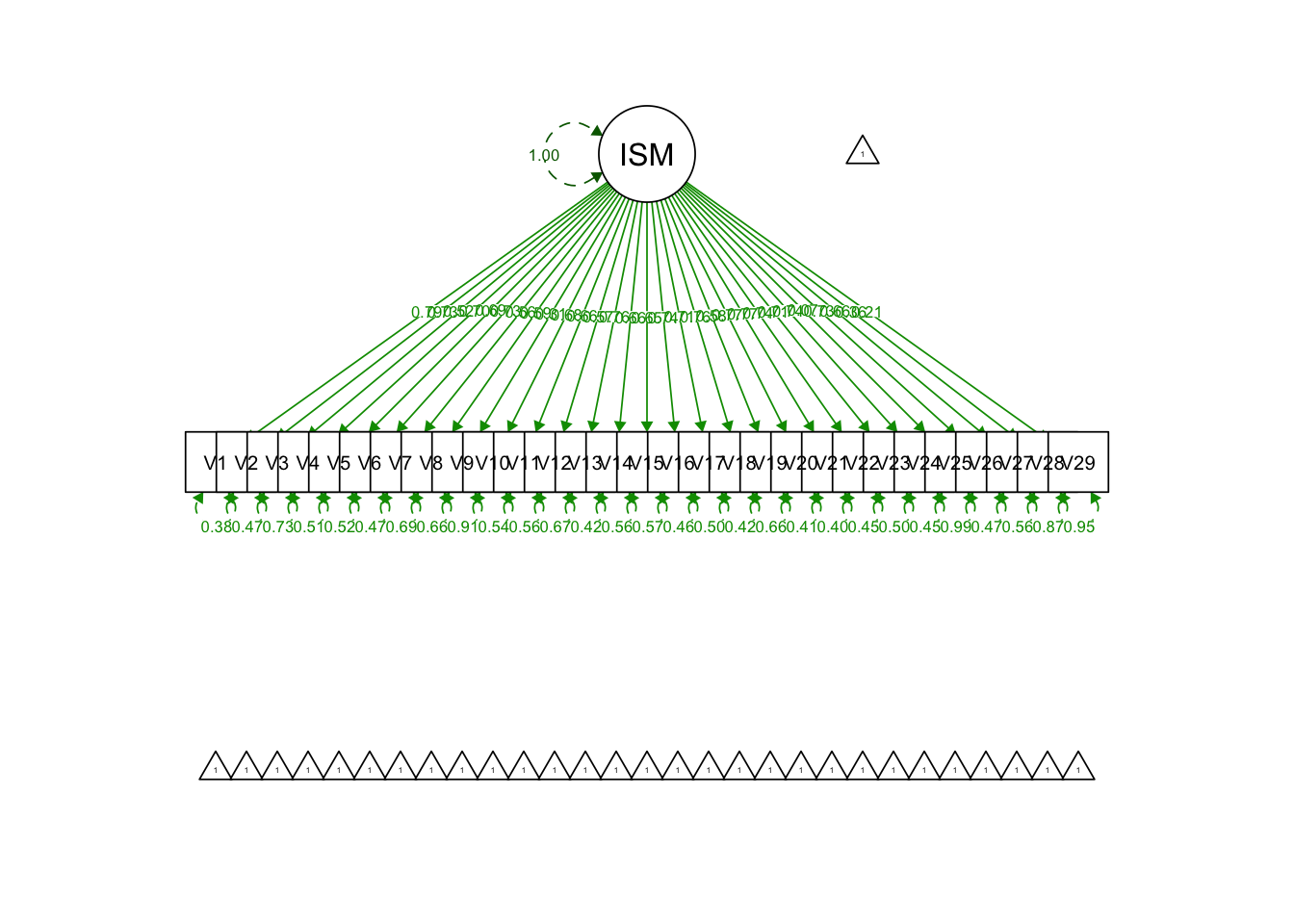
20.3 PART III: Second-order factor Model
Write out syntax for a five-factor second-order CFA model:
secondfac.model = '
Alienation =~ V1+V2+V3+V4+V5+V6
Stereotype =~ V7+V8+V9+V10+V11+V12+V13
Discrimination =~ V14+V15+V16+V17+V18
Withdrawal =~ V19+V20+V21+V22+V23+V24
Stigma =~ V25+V26+V27+V28+V29
# Second-order factor ISMI
ISMI =~ Alienation + Stereotype + Discrimination + Withdrawal + Stigma
'secondfac.model.fit = lavaan::sem(secondfac.model,
data=ISMI29,
ordered = colnames(ISMI29),
std.lv = TRUE,
fixed.x = F)
summary(secondfac.model.fit, standardized = TRUE, fit.measures = TRUE)## lavaan 0.6-12 ended normally after 139 iterations
##
## Estimator DWLS
## Optimization method NLMINB
## Number of model parameters 121
##
## Number of observations 758
##
## Model Test User Model:
## Standard Robust
## Test Statistic 1550.644 1966.260
## Degrees of freedom 372 372
## P-value (Chi-square) 0.000 0.000
## Scaling correction factor 0.848
## Shift parameter 138.291
## simple second-order correction
##
## Model Test Baseline Model:
##
## Test statistic 76016.286 21485.170
## Degrees of freedom 406 406
## P-value 0.000 0.000
## Scaling correction factor 3.587
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.984 0.924
## Tucker-Lewis Index (TLI) 0.983 0.917
##
## Robust Comparative Fit Index (CFI) NA
## Robust Tucker-Lewis Index (TLI) NA
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.065 0.075
## 90 Percent confidence interval - lower 0.061 0.072
## 90 Percent confidence interval - upper 0.068 0.079
## P-value RMSEA <= 0.05 0.000 0.000
##
## Robust RMSEA NA
## 90 Percent confidence interval - lower NA
## 90 Percent confidence interval - upper NA
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.064 0.064
##
## Parameter Estimates:
##
## Standard errors Robust.sem
## Information Expected
## Information saturated (h1) model Unstructured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv
## Alienation =~
## V1 0.337 0.022 15.037 0.000 0.839
## V2 0.312 0.021 15.081 0.000 0.776
## V3 0.223 0.017 13.259 0.000 0.556
## V4 0.298 0.019 15.597 0.000 0.742
## V5 0.295 0.019 15.793 0.000 0.735
## V6 0.310 0.020 15.515 0.000 0.772
## Stereotype =~
## V7 0.279 0.020 13.715 0.000 0.613
## V8 0.292 0.022 13.523 0.000 0.643
## V9 0.155 0.020 7.585 0.000 0.340
## V10 0.336 0.022 15.118 0.000 0.739
## V11 0.330 0.022 15.229 0.000 0.725
## V12 0.284 0.021 13.434 0.000 0.625
## V13 0.379 0.024 15.594 0.000 0.833
## Discrimination =~
## V14 0.377 0.018 20.832 0.000 0.727
## V15 0.373 0.018 20.422 0.000 0.720
## V16 0.420 0.019 22.443 0.000 0.810
## V17 0.402 0.018 21.813 0.000 0.776
## V18 0.442 0.024 18.275 0.000 0.853
## Withdrawal =~
## V19 0.185 0.019 9.612 0.000 0.609
## V20 0.243 0.023 10.420 0.000 0.801
## V21 0.245 0.024 10.093 0.000 0.809
## V22 0.235 0.023 10.395 0.000 0.775
## V23 0.225 0.023 9.963 0.000 0.743
## V24 0.234 0.023 10.186 0.000 0.772
## Stigma =~
## V25 0.036 0.018 1.967 0.049 0.082
## V26 0.357 0.031 11.708 0.000 0.815
## V27 0.325 0.027 11.913 0.000 0.742
## V28 0.175 0.022 8.005 0.000 0.400
## V29 0.105 0.018 5.830 0.000 0.241
## ISMI =~
## Alienation 2.281 0.168 13.578 0.000 0.916
## Stereotype 1.958 0.147 13.316 0.000 0.891
## Discrimination 1.651 0.104 15.930 0.000 0.855
## Withdrawal 3.144 0.332 9.469 0.000 0.953
## Stigma 2.050 0.195 10.535 0.000 0.899
## Std.all
##
## 0.839
## 0.776
## 0.556
## 0.742
## 0.735
## 0.772
##
## 0.613
## 0.643
## 0.340
## 0.739
## 0.725
## 0.625
## 0.833
##
## 0.727
## 0.720
## 0.810
## 0.776
## 0.853
##
## 0.609
## 0.801
## 0.809
## 0.775
## 0.743
## 0.772
##
## 0.082
## 0.815
## 0.742
## 0.400
## 0.241
##
## 0.916
## 0.891
## 0.855
## 0.953
## 0.899
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv
## .V1 0.000 0.000
## .V2 0.000 0.000
## .V3 0.000 0.000
## .V4 0.000 0.000
## .V5 0.000 0.000
## .V6 0.000 0.000
## .V7 0.000 0.000
## .V8 0.000 0.000
## .V9 0.000 0.000
## .V10 0.000 0.000
## .V11 0.000 0.000
## .V12 0.000 0.000
## .V13 0.000 0.000
## .V14 0.000 0.000
## .V15 0.000 0.000
## .V16 0.000 0.000
## .V17 0.000 0.000
## .V18 0.000 0.000
## .V19 0.000 0.000
## .V20 0.000 0.000
## .V21 0.000 0.000
## .V22 0.000 0.000
## .V23 0.000 0.000
## .V24 0.000 0.000
## .V25 0.000 0.000
## .V26 0.000 0.000
## .V27 0.000 0.000
## .V28 0.000 0.000
## .V29 0.000 0.000
## .Alienation 0.000 0.000
## .Stereotype 0.000 0.000
## .Discrimination 0.000 0.000
## .Withdrawal 0.000 0.000
## .Stigma 0.000 0.000
## ISMI 0.000 0.000
## Std.all
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
##
## Thresholds:
## Estimate Std.Err z-value P(>|z|) Std.lv
## V1|t1 -0.980 0.054 -17.991 0.000 -0.980
## V1|t2 -0.099 0.046 -2.178 0.029 -0.099
## V1|t3 1.046 0.056 18.722 0.000 1.046
## V2|t1 -0.903 0.053 -17.036 0.000 -0.903
## V2|t2 0.213 0.046 4.643 0.000 0.213
## V2|t3 1.202 0.060 20.103 0.000 1.202
## V3|t1 -1.149 0.058 -19.687 0.000 -1.149
## V3|t2 -0.070 0.046 -1.524 0.127 -0.070
## V3|t3 1.175 0.059 19.899 0.000 1.175
## V4|t1 -0.985 0.055 -18.053 0.000 -0.985
## V4|t2 -0.066 0.046 -1.452 0.147 -0.066
## V4|t3 1.058 0.056 18.840 0.000 1.058
## V5|t1 -0.785 0.051 -15.374 0.000 -0.785
## V5|t2 -0.046 0.046 -1.016 0.309 -0.046
## V5|t3 1.029 0.056 18.542 0.000 1.029
## V6|t1 -0.758 0.051 -14.965 0.000 -0.758
## V6|t2 0.060 0.046 1.307 0.191 0.060
## V6|t3 1.202 0.060 20.103 0.000 1.202
## V7|t1 -0.685 0.050 -13.793 0.000 -0.685
## V7|t2 0.537 0.048 11.189 0.000 0.537
## V7|t3 1.711 0.080 21.292 0.000 1.711
## V8|t1 0.404 0.047 8.614 0.000 0.404
## V8|t2 1.606 0.075 21.452 0.000 1.606
## V8|t3 2.183 0.118 18.488 0.000 2.183
## V9|t1 0.264 0.046 5.729 0.000 0.264
## V9|t2 1.711 0.080 21.292 0.000 1.711
## V9|t3 2.656 0.194 13.656 0.000 2.656
## V10|t1 0.261 0.046 5.656 0.000 0.261
## V10|t2 1.429 0.067 21.257 0.000 1.429
## V10|t3 2.149 0.114 18.786 0.000 2.149
## V11|t1 0.073 0.046 1.597 0.110 0.073
## V11|t2 1.319 0.063 20.826 0.000 1.319
## V11|t3 2.261 0.127 17.776 0.000 2.261
## V12|t1 0.507 0.048 10.619 0.000 0.507
## V12|t2 1.839 0.088 20.845 0.000 1.839
## V12|t3 2.413 0.148 16.268 0.000 2.413
## V13|t1 0.288 0.046 6.235 0.000 0.288
## V13|t2 1.438 0.068 21.282 0.000 1.438
## V13|t3 2.031 0.103 19.706 0.000 2.031
## V14|t1 -0.632 0.049 -12.885 0.000 -0.632
## V14|t2 0.496 0.048 10.405 0.000 0.496
## V14|t3 1.476 0.069 21.369 0.000 1.476
## V15|t1 -0.401 0.047 -8.542 0.000 -0.401
## V15|t2 0.771 0.051 15.170 0.000 0.771
## V15|t3 1.726 0.081 21.255 0.000 1.726
## V16|t1 -0.557 0.048 -11.544 0.000 -0.557
## V16|t2 0.534 0.048 11.118 0.000 0.534
## V16|t3 1.549 0.072 21.455 0.000 1.549
## V17|t1 -0.285 0.046 -6.162 0.000 -0.285
## V17|t2 0.803 0.051 15.644 0.000 0.803
## V17|t3 1.771 0.084 21.114 0.000 1.771
## V18|t1 -0.437 0.047 -9.260 0.000 -0.437
## V18|t2 0.632 0.049 12.885 0.000 0.632
## V18|t3 1.726 0.081 21.255 0.000 1.726
## V19|t1 -1.243 0.061 -20.393 0.000 -1.243
## V19|t2 -0.210 0.046 -4.570 0.000 -0.210
## V19|t3 0.888 0.053 16.840 0.000 0.888
## V20|t1 -0.664 0.049 -13.445 0.000 -0.664
## V20|t2 0.278 0.046 6.018 0.000 0.278
## V20|t3 1.251 0.061 20.439 0.000 1.251
## V21|t1 -0.727 0.050 -14.485 0.000 -0.727
## V21|t2 0.433 0.047 9.189 0.000 0.433
## V21|t3 1.517 0.071 21.429 0.000 1.517
## V22|t1 -0.261 0.046 -5.656 0.000 -0.261
## V22|t2 0.758 0.051 14.965 0.000 0.758
## V22|t3 1.656 0.077 21.400 0.000 1.656
## V23|t1 -0.572 0.048 -11.827 0.000 -0.572
## V23|t2 0.440 0.047 9.332 0.000 0.440
## V23|t3 1.447 0.068 21.306 0.000 1.447
## V24|t1 -0.323 0.046 -6.957 0.000 -0.323
## V24|t2 0.789 0.051 15.441 0.000 0.789
## V24|t3 1.571 0.073 21.461 0.000 1.571
## V25|t1 -0.873 0.052 -16.644 0.000 -0.873
## V25|t2 0.437 0.047 9.260 0.000 0.437
## V25|t3 1.420 0.067 21.231 0.000 1.420
## V26|t1 -1.001 0.055 -18.238 0.000 -1.001
## V26|t2 0.306 0.046 6.596 0.000 0.306
## V26|t3 1.236 0.061 20.346 0.000 1.236
## V27|t1 -0.481 0.048 -10.120 0.000 -0.481
## V27|t2 0.854 0.052 16.380 0.000 0.854
## V27|t3 1.683 0.079 21.354 0.000 1.683
## V28|t1 0.254 0.046 5.512 0.000 0.254
## V28|t2 1.656 0.077 21.400 0.000 1.656
## V28|t3 1.982 0.099 20.046 0.000 1.982
## V29|t1 -0.698 0.050 -14.001 0.000 -0.698
## V29|t2 0.619 0.049 12.674 0.000 0.619
## V29|t3 1.756 0.083 21.166 0.000 1.756
## Std.all
## -0.980
## -0.099
## 1.046
## -0.903
## 0.213
## 1.202
## -1.149
## -0.070
## 1.175
## -0.985
## -0.066
## 1.058
## -0.785
## -0.046
## 1.029
## -0.758
## 0.060
## 1.202
## -0.685
## 0.537
## 1.711
## 0.404
## 1.606
## 2.183
## 0.264
## 1.711
## 2.656
## 0.261
## 1.429
## 2.149
## 0.073
## 1.319
## 2.261
## 0.507
## 1.839
## 2.413
## 0.288
## 1.438
## 2.031
## -0.632
## 0.496
## 1.476
## -0.401
## 0.771
## 1.726
## -0.557
## 0.534
## 1.549
## -0.285
## 0.803
## 1.771
## -0.437
## 0.632
## 1.726
## -1.243
## -0.210
## 0.888
## -0.664
## 0.278
## 1.251
## -0.727
## 0.433
## 1.517
## -0.261
## 0.758
## 1.656
## -0.572
## 0.440
## 1.447
## -0.323
## 0.789
## 1.571
## -0.873
## 0.437
## 1.420
## -1.001
## 0.306
## 1.236
## -0.481
## 0.854
## 1.683
## 0.254
## 1.656
## 1.982
## -0.698
## 0.619
## 1.756
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv
## .V1 0.295 0.295
## .V2 0.398 0.398
## .V3 0.691 0.691
## .V4 0.449 0.449
## .V5 0.460 0.460
## .V6 0.403 0.403
## .V7 0.624 0.624
## .V8 0.587 0.587
## .V9 0.885 0.885
## .V10 0.453 0.453
## .V11 0.475 0.475
## .V12 0.610 0.610
## .V13 0.307 0.307
## .V14 0.472 0.472
## .V15 0.482 0.482
## .V16 0.344 0.344
## .V17 0.397 0.397
## .V18 0.273 0.273
## .V19 0.629 0.629
## .V20 0.359 0.359
## .V21 0.346 0.346
## .V22 0.399 0.399
## .V23 0.449 0.449
## .V24 0.404 0.404
## .V25 0.993 0.993
## .V26 0.336 0.336
## .V27 0.450 0.450
## .V28 0.840 0.840
## .V29 0.942 0.942
## .Alienation 1.000 0.161
## .Stereotype 1.000 0.207
## .Discrimination 1.000 0.268
## .Withdrawal 1.000 0.092
## .Stigma 1.000 0.192
## ISMI 1.000 1.000
## Std.all
## 0.295
## 0.398
## 0.691
## 0.449
## 0.460
## 0.403
## 0.624
## 0.587
## 0.885
## 0.453
## 0.475
## 0.610
## 0.307
## 0.472
## 0.482
## 0.344
## 0.397
## 0.273
## 0.629
## 0.359
## 0.346
## 0.399
## 0.449
## 0.404
## 0.993
## 0.336
## 0.450
## 0.840
## 0.942
## 0.161
## 0.207
## 0.268
## 0.092
## 0.192
## 1.000
##
## Scales y*:
## Estimate Std.Err z-value P(>|z|) Std.lv
## V1 1.000 1.000
## V2 1.000 1.000
## V3 1.000 1.000
## V4 1.000 1.000
## V5 1.000 1.000
## V6 1.000 1.000
## V7 1.000 1.000
## V8 1.000 1.000
## V9 1.000 1.000
## V10 1.000 1.000
## V11 1.000 1.000
## V12 1.000 1.000
## V13 1.000 1.000
## V14 1.000 1.000
## V15 1.000 1.000
## V16 1.000 1.000
## V17 1.000 1.000
## V18 1.000 1.000
## V19 1.000 1.000
## V20 1.000 1.000
## V21 1.000 1.000
## V22 1.000 1.000
## V23 1.000 1.000
## V24 1.000 1.000
## V25 1.000 1.000
## V26 1.000 1.000
## V27 1.000 1.000
## V28 1.000 1.000
## V29 1.000 1.000
## Std.all
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000semPaths(secondfac.model.fit, what = 'std', fade = F)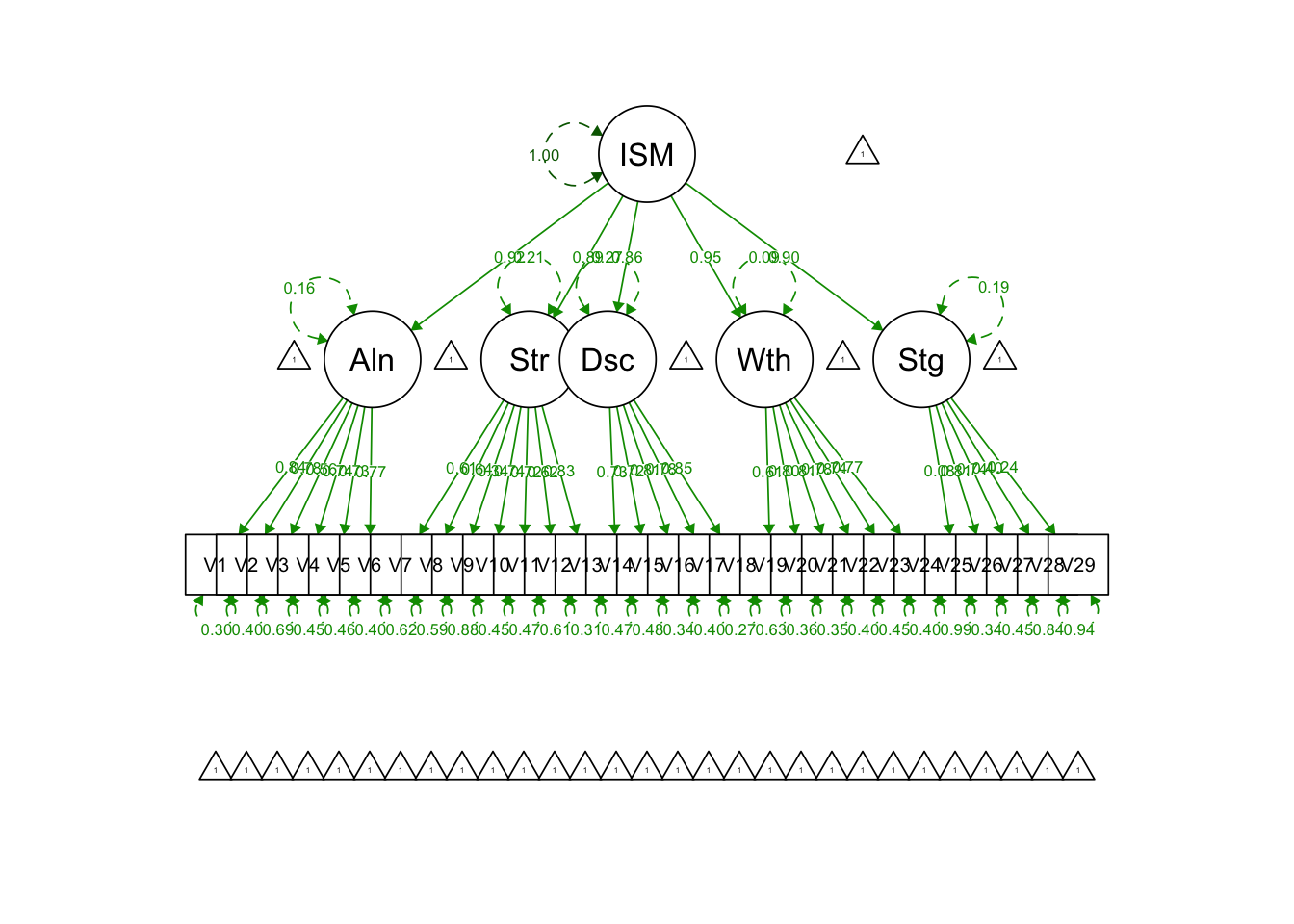
20.4 PART IV: Bifactor Model
bifac.model = '
# specific factors
Alienation =~ V1+V2+V3+V4+V5+V6
Stereotype =~ V7+V8+V9+V10+V11+V12+V13
Discrimination =~ V14+V15+V16+V17+V18
Withdrawal =~ V19+V20+V21+V22+V23+V24
Stigma =~ V25+V26+V27+V28+V29
# general factor GEN
GEN =~ V1+V2+V3+V4+V5+V6+V7+V8+V9+V10+V11+V12+V13+V14+V15+V16+V17+V18+V19+
V20+V21+V22+V23+V24+V25+V26+V27+V28+V29
'When using sem() to fit a bifactor model, make sure to turn on
- orthogonal = TRUE to ensure that all specific factors and general factors are uncorrelated
- otherwise, you’ll get an error/warning saying that the model is not identified.
bifac.model.fit = lavaan::sem(bifac.model,
data=ISMI29,
ordered = colnames(ISMI29),
std.lv = TRUE,
fixed.x = F,
orthogonal = TRUE)summary(bifac.model.fit, standardized = TRUE, fit.measures = TRUE)## lavaan 0.6-12 ended normally after 74 iterations
##
## Estimator DWLS
## Optimization method NLMINB
## Number of model parameters 145
##
## Number of observations 758
##
## Model Test User Model:
## Standard Robust
## Test Statistic 1062.671 1472.549
## Degrees of freedom 348 348
## P-value (Chi-square) 0.000 0.000
## Scaling correction factor 0.788
## Shift parameter 123.999
## simple second-order correction
##
## Model Test Baseline Model:
##
## Test statistic 76016.286 21485.170
## Degrees of freedom 406 406
## P-value 0.000 0.000
## Scaling correction factor 3.587
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.991 0.947
## Tucker-Lewis Index (TLI) 0.989 0.938
##
## Robust Comparative Fit Index (CFI) NA
## Robust Tucker-Lewis Index (TLI) NA
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.052 0.065
## 90 Percent confidence interval - lower 0.049 0.062
## 90 Percent confidence interval - upper 0.056 0.069
## P-value RMSEA <= 0.05 0.165 0.000
##
## Robust RMSEA NA
## 90 Percent confidence interval - lower NA
## 90 Percent confidence interval - upper NA
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.054 0.054
##
## Parameter Estimates:
##
## Standard errors Robust.sem
## Information Expected
## Information saturated (h1) model Unstructured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv
## Alienation =~
## V1 0.085 0.035 2.439 0.015 0.085
## V2 0.147 0.036 4.126 0.000 0.147
## V3 0.040 0.045 0.898 0.369 0.040
## V4 0.474 0.038 12.601 0.000 0.474
## V5 0.527 0.039 13.557 0.000 0.527
## V6 0.393 0.035 11.194 0.000 0.393
## Stereotype =~
## V7 0.116 0.047 2.479 0.013 0.116
## V8 0.210 0.049 4.272 0.000 0.210
## V9 0.438 0.057 7.744 0.000 0.438
## V10 0.274 0.042 6.544 0.000 0.274
## V11 0.398 0.037 10.611 0.000 0.398
## V12 0.563 0.056 10.012 0.000 0.563
## V13 0.271 0.038 7.086 0.000 0.271
## Discrimination =~
## V14 0.495 0.032 15.564 0.000 0.495
## V15 0.477 0.033 14.494 0.000 0.477
## V16 0.554 0.032 17.388 0.000 0.554
## V17 0.482 0.033 14.624 0.000 0.482
## V18 -0.032 0.032 -1.008 0.313 -0.032
## Withdrawal =~
## V19 0.172 0.048 3.606 0.000 0.172
## V20 0.465 0.058 8.050 0.000 0.465
## V21 0.082 0.040 2.054 0.040 0.082
## V22 0.358 0.052 6.888 0.000 0.358
## V23 0.107 0.046 2.330 0.020 0.107
## V24 0.218 0.042 5.185 0.000 0.218
## Stigma =~
## V25 0.404 0.066 6.138 0.000 0.404
## V26 0.056 0.040 1.414 0.157 0.056
## V27 0.291 0.048 6.086 0.000 0.291
## V28 0.483 0.067 7.201 0.000 0.483
## V29 0.349 0.061 5.752 0.000 0.349
## GEN =~
## V1 0.797 0.016 49.723 0.000 0.797
## V2 0.730 0.019 39.263 0.000 0.730
## V3 0.532 0.028 19.069 0.000 0.532
## V4 0.657 0.022 30.128 0.000 0.657
## V5 0.646 0.023 27.532 0.000 0.646
## V6 0.697 0.020 34.750 0.000 0.697
## V7 0.561 0.028 20.047 0.000 0.561
## V8 0.581 0.034 17.084 0.000 0.581
## V9 0.267 0.041 6.586 0.000 0.267
## V10 0.666 0.028 23.951 0.000 0.666
## V11 0.638 0.026 24.148 0.000 0.638
## V12 0.521 0.038 13.851 0.000 0.521
## V13 0.750 0.025 30.069 0.000 0.750
## V14 0.600 0.026 23.101 0.000 0.600
## V15 0.595 0.027 22.367 0.000 0.595
## V16 0.667 0.023 28.805 0.000 0.667
## V17 0.647 0.024 26.442 0.000 0.647
## V18 0.787 0.017 45.401 0.000 0.787
## V19 0.581 0.026 22.230 0.000 0.581
## V20 0.743 0.019 39.129 0.000 0.743
## V21 0.785 0.018 44.861 0.000 0.785
## V22 0.723 0.021 34.234 0.000 0.723
## V23 0.718 0.021 33.856 0.000 0.718
## V24 0.735 0.020 36.129 0.000 0.735
## V25 0.056 0.039 1.451 0.147 0.056
## V26 0.742 0.020 37.899 0.000 0.742
## V27 0.673 0.024 27.596 0.000 0.673
## V28 0.351 0.039 8.996 0.000 0.351
## V29 0.206 0.037 5.619 0.000 0.206
## Std.all
##
## 0.085
## 0.147
## 0.040
## 0.474
## 0.527
## 0.393
##
## 0.116
## 0.210
## 0.438
## 0.274
## 0.398
## 0.563
## 0.271
##
## 0.495
## 0.477
## 0.554
## 0.482
## -0.032
##
## 0.172
## 0.465
## 0.082
## 0.358
## 0.107
## 0.218
##
## 0.404
## 0.056
## 0.291
## 0.483
## 0.349
##
## 0.797
## 0.730
## 0.532
## 0.657
## 0.646
## 0.697
## 0.561
## 0.581
## 0.267
## 0.666
## 0.638
## 0.521
## 0.750
## 0.600
## 0.595
## 0.667
## 0.647
## 0.787
## 0.581
## 0.743
## 0.785
## 0.723
## 0.718
## 0.735
## 0.056
## 0.742
## 0.673
## 0.351
## 0.206
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv
## Alienation ~~
## Stereotype 0.000 0.000
## Discrimination 0.000 0.000
## Withdrawal 0.000 0.000
## Stigma 0.000 0.000
## GEN 0.000 0.000
## Stereotype ~~
## Discrimination 0.000 0.000
## Withdrawal 0.000 0.000
## Stigma 0.000 0.000
## GEN 0.000 0.000
## Discrimination ~~
## Withdrawal 0.000 0.000
## Stigma 0.000 0.000
## GEN 0.000 0.000
## Withdrawal ~~
## Stigma 0.000 0.000
## GEN 0.000 0.000
## Stigma ~~
## GEN 0.000 0.000
## Std.all
##
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
##
## 0.000
## 0.000
## 0.000
## 0.000
##
## 0.000
## 0.000
## 0.000
##
## 0.000
## 0.000
##
## 0.000
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv
## .V1 0.000 0.000
## .V2 0.000 0.000
## .V3 0.000 0.000
## .V4 0.000 0.000
## .V5 0.000 0.000
## .V6 0.000 0.000
## .V7 0.000 0.000
## .V8 0.000 0.000
## .V9 0.000 0.000
## .V10 0.000 0.000
## .V11 0.000 0.000
## .V12 0.000 0.000
## .V13 0.000 0.000
## .V14 0.000 0.000
## .V15 0.000 0.000
## .V16 0.000 0.000
## .V17 0.000 0.000
## .V18 0.000 0.000
## .V19 0.000 0.000
## .V20 0.000 0.000
## .V21 0.000 0.000
## .V22 0.000 0.000
## .V23 0.000 0.000
## .V24 0.000 0.000
## .V25 0.000 0.000
## .V26 0.000 0.000
## .V27 0.000 0.000
## .V28 0.000 0.000
## .V29 0.000 0.000
## Alienation 0.000 0.000
## Stereotype 0.000 0.000
## Discrimination 0.000 0.000
## Withdrawal 0.000 0.000
## Stigma 0.000 0.000
## GEN 0.000 0.000
## Std.all
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
## 0.000
##
## Thresholds:
## Estimate Std.Err z-value P(>|z|) Std.lv
## V1|t1 -0.980 0.054 -17.991 0.000 -0.980
## V1|t2 -0.099 0.046 -2.178 0.029 -0.099
## V1|t3 1.046 0.056 18.722 0.000 1.046
## V2|t1 -0.903 0.053 -17.036 0.000 -0.903
## V2|t2 0.213 0.046 4.643 0.000 0.213
## V2|t3 1.202 0.060 20.103 0.000 1.202
## V3|t1 -1.149 0.058 -19.687 0.000 -1.149
## V3|t2 -0.070 0.046 -1.524 0.127 -0.070
## V3|t3 1.175 0.059 19.899 0.000 1.175
## V4|t1 -0.985 0.055 -18.053 0.000 -0.985
## V4|t2 -0.066 0.046 -1.452 0.147 -0.066
## V4|t3 1.058 0.056 18.840 0.000 1.058
## V5|t1 -0.785 0.051 -15.374 0.000 -0.785
## V5|t2 -0.046 0.046 -1.016 0.309 -0.046
## V5|t3 1.029 0.056 18.542 0.000 1.029
## V6|t1 -0.758 0.051 -14.965 0.000 -0.758
## V6|t2 0.060 0.046 1.307 0.191 0.060
## V6|t3 1.202 0.060 20.103 0.000 1.202
## V7|t1 -0.685 0.050 -13.793 0.000 -0.685
## V7|t2 0.537 0.048 11.189 0.000 0.537
## V7|t3 1.711 0.080 21.292 0.000 1.711
## V8|t1 0.404 0.047 8.614 0.000 0.404
## V8|t2 1.606 0.075 21.452 0.000 1.606
## V8|t3 2.183 0.118 18.488 0.000 2.183
## V9|t1 0.264 0.046 5.729 0.000 0.264
## V9|t2 1.711 0.080 21.292 0.000 1.711
## V9|t3 2.656 0.194 13.656 0.000 2.656
## V10|t1 0.261 0.046 5.656 0.000 0.261
## V10|t2 1.429 0.067 21.257 0.000 1.429
## V10|t3 2.149 0.114 18.786 0.000 2.149
## V11|t1 0.073 0.046 1.597 0.110 0.073
## V11|t2 1.319 0.063 20.826 0.000 1.319
## V11|t3 2.261 0.127 17.776 0.000 2.261
## V12|t1 0.507 0.048 10.619 0.000 0.507
## V12|t2 1.839 0.088 20.845 0.000 1.839
## V12|t3 2.413 0.148 16.268 0.000 2.413
## V13|t1 0.288 0.046 6.235 0.000 0.288
## V13|t2 1.438 0.068 21.282 0.000 1.438
## V13|t3 2.031 0.103 19.706 0.000 2.031
## V14|t1 -0.632 0.049 -12.885 0.000 -0.632
## V14|t2 0.496 0.048 10.405 0.000 0.496
## V14|t3 1.476 0.069 21.369 0.000 1.476
## V15|t1 -0.401 0.047 -8.542 0.000 -0.401
## V15|t2 0.771 0.051 15.170 0.000 0.771
## V15|t3 1.726 0.081 21.255 0.000 1.726
## V16|t1 -0.557 0.048 -11.544 0.000 -0.557
## V16|t2 0.534 0.048 11.118 0.000 0.534
## V16|t3 1.549 0.072 21.455 0.000 1.549
## V17|t1 -0.285 0.046 -6.162 0.000 -0.285
## V17|t2 0.803 0.051 15.644 0.000 0.803
## V17|t3 1.771 0.084 21.114 0.000 1.771
## V18|t1 -0.437 0.047 -9.260 0.000 -0.437
## V18|t2 0.632 0.049 12.885 0.000 0.632
## V18|t3 1.726 0.081 21.255 0.000 1.726
## V19|t1 -1.243 0.061 -20.393 0.000 -1.243
## V19|t2 -0.210 0.046 -4.570 0.000 -0.210
## V19|t3 0.888 0.053 16.840 0.000 0.888
## V20|t1 -0.664 0.049 -13.445 0.000 -0.664
## V20|t2 0.278 0.046 6.018 0.000 0.278
## V20|t3 1.251 0.061 20.439 0.000 1.251
## V21|t1 -0.727 0.050 -14.485 0.000 -0.727
## V21|t2 0.433 0.047 9.189 0.000 0.433
## V21|t3 1.517 0.071 21.429 0.000 1.517
## V22|t1 -0.261 0.046 -5.656 0.000 -0.261
## V22|t2 0.758 0.051 14.965 0.000 0.758
## V22|t3 1.656 0.077 21.400 0.000 1.656
## V23|t1 -0.572 0.048 -11.827 0.000 -0.572
## V23|t2 0.440 0.047 9.332 0.000 0.440
## V23|t3 1.447 0.068 21.306 0.000 1.447
## V24|t1 -0.323 0.046 -6.957 0.000 -0.323
## V24|t2 0.789 0.051 15.441 0.000 0.789
## V24|t3 1.571 0.073 21.461 0.000 1.571
## V25|t1 -0.873 0.052 -16.644 0.000 -0.873
## V25|t2 0.437 0.047 9.260 0.000 0.437
## V25|t3 1.420 0.067 21.231 0.000 1.420
## V26|t1 -1.001 0.055 -18.238 0.000 -1.001
## V26|t2 0.306 0.046 6.596 0.000 0.306
## V26|t3 1.236 0.061 20.346 0.000 1.236
## V27|t1 -0.481 0.048 -10.120 0.000 -0.481
## V27|t2 0.854 0.052 16.380 0.000 0.854
## V27|t3 1.683 0.079 21.354 0.000 1.683
## V28|t1 0.254 0.046 5.512 0.000 0.254
## V28|t2 1.656 0.077 21.400 0.000 1.656
## V28|t3 1.982 0.099 20.046 0.000 1.982
## V29|t1 -0.698 0.050 -14.001 0.000 -0.698
## V29|t2 0.619 0.049 12.674 0.000 0.619
## V29|t3 1.756 0.083 21.166 0.000 1.756
## Std.all
## -0.980
## -0.099
## 1.046
## -0.903
## 0.213
## 1.202
## -1.149
## -0.070
## 1.175
## -0.985
## -0.066
## 1.058
## -0.785
## -0.046
## 1.029
## -0.758
## 0.060
## 1.202
## -0.685
## 0.537
## 1.711
## 0.404
## 1.606
## 2.183
## 0.264
## 1.711
## 2.656
## 0.261
## 1.429
## 2.149
## 0.073
## 1.319
## 2.261
## 0.507
## 1.839
## 2.413
## 0.288
## 1.438
## 2.031
## -0.632
## 0.496
## 1.476
## -0.401
## 0.771
## 1.726
## -0.557
## 0.534
## 1.549
## -0.285
## 0.803
## 1.771
## -0.437
## 0.632
## 1.726
## -1.243
## -0.210
## 0.888
## -0.664
## 0.278
## 1.251
## -0.727
## 0.433
## 1.517
## -0.261
## 0.758
## 1.656
## -0.572
## 0.440
## 1.447
## -0.323
## 0.789
## 1.571
## -0.873
## 0.437
## 1.420
## -1.001
## 0.306
## 1.236
## -0.481
## 0.854
## 1.683
## 0.254
## 1.656
## 1.982
## -0.698
## 0.619
## 1.756
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv
## .V1 0.358 0.358
## .V2 0.445 0.445
## .V3 0.715 0.715
## .V4 0.343 0.343
## .V5 0.305 0.305
## .V6 0.360 0.360
## .V7 0.672 0.672
## .V8 0.618 0.618
## .V9 0.736 0.736
## .V10 0.482 0.482
## .V11 0.435 0.435
## .V12 0.411 0.411
## .V13 0.364 0.364
## .V14 0.395 0.395
## .V15 0.419 0.419
## .V16 0.248 0.248
## .V17 0.348 0.348
## .V18 0.379 0.379
## .V19 0.633 0.633
## .V20 0.232 0.232
## .V21 0.377 0.377
## .V22 0.349 0.349
## .V23 0.473 0.473
## .V24 0.413 0.413
## .V25 0.833 0.833
## .V26 0.446 0.446
## .V27 0.462 0.462
## .V28 0.643 0.643
## .V29 0.836 0.836
## Alienation 1.000 1.000
## Stereotype 1.000 1.000
## Discrimination 1.000 1.000
## Withdrawal 1.000 1.000
## Stigma 1.000 1.000
## GEN 1.000 1.000
## Std.all
## 0.358
## 0.445
## 0.715
## 0.343
## 0.305
## 0.360
## 0.672
## 0.618
## 0.736
## 0.482
## 0.435
## 0.411
## 0.364
## 0.395
## 0.419
## 0.248
## 0.348
## 0.379
## 0.633
## 0.232
## 0.377
## 0.349
## 0.473
## 0.413
## 0.833
## 0.446
## 0.462
## 0.643
## 0.836
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
##
## Scales y*:
## Estimate Std.Err z-value P(>|z|) Std.lv
## V1 1.000 1.000
## V2 1.000 1.000
## V3 1.000 1.000
## V4 1.000 1.000
## V5 1.000 1.000
## V6 1.000 1.000
## V7 1.000 1.000
## V8 1.000 1.000
## V9 1.000 1.000
## V10 1.000 1.000
## V11 1.000 1.000
## V12 1.000 1.000
## V13 1.000 1.000
## V14 1.000 1.000
## V15 1.000 1.000
## V16 1.000 1.000
## V17 1.000 1.000
## V18 1.000 1.000
## V19 1.000 1.000
## V20 1.000 1.000
## V21 1.000 1.000
## V22 1.000 1.000
## V23 1.000 1.000
## V24 1.000 1.000
## V25 1.000 1.000
## V26 1.000 1.000
## V27 1.000 1.000
## V28 1.000 1.000
## V29 1.000 1.000
## Std.all
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000
## 1.000semPaths(bifac.model.fit, what = 'std', fade = F)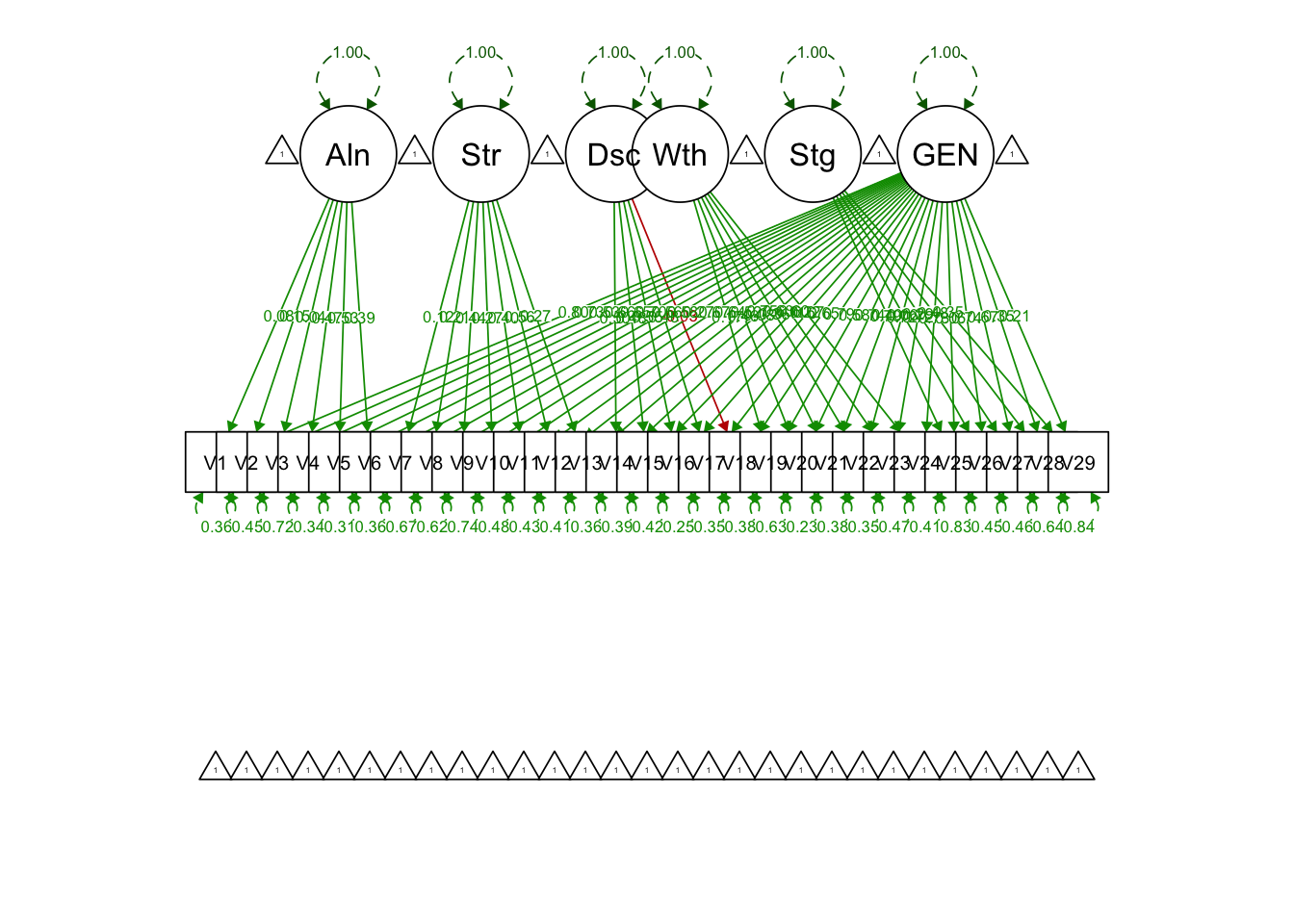
20.5 PART V: Model Comparison
UniFactor = fitMeasures(uni.model.fit, fit.measures = c("chisq.scaled", "df.scaled", "pvalue.scaled", "rmsea.scaled", "rmsea.ci.lower.scaled", "rmsea.ci.upper.scaled", "cfi.scaled", "tli.scaled", "srmr_bentler"))
FiveFactor = fitMeasures(cor.fac.model.fit, fit.measures = c("chisq.scaled", "df.scaled", "pvalue.scaled", "rmsea.scaled", "rmsea.ci.lower.scaled", "rmsea.ci.upper.scaled", "cfi.scaled", "tli.scaled", "srmr_bentler"))
SecondOrder = fitMeasures(secondfac.model.fit, fit.measures = c("chisq.scaled", "df.scaled", "pvalue.scaled", "rmsea.scaled", "rmsea.ci.lower.scaled", "rmsea.ci.upper.scaled", "cfi.scaled", "tli.scaled", "srmr_bentler"))
Bifactor = fitMeasures(bifac.model.fit, fit.measures = c("chisq.scaled", "df.scaled", "pvalue.scaled", "rmsea.scaled", "rmsea.ci.lower.scaled", "rmsea.ci.upper.scaled", "cfi.scaled", "tli.scaled", "srmr_bentler"))
round(cbind(UniFactor, FiveFactor, SecondOrder, Bifactor), 3)## UniFactor FiveFactor SecondOrder Bifactor
## chisq.scaled 2606.734 1751.387 1966.260 1472.549
## df.scaled 377.000 367.000 372.000 348.000
## pvalue.scaled 0.000 0.000 0.000 0.000
## rmsea.scaled 0.088 0.071 0.075 0.065
## rmsea.ci.lower.scaled 0.085 0.067 0.072 0.062
## rmsea.ci.upper.scaled 0.092 0.074 0.079 0.069
## cfi.scaled 0.894 0.934 0.924 0.947
## tli.scaled 0.886 0.927 0.917 0.938Bifactor model wins!
20.6 Exercise: Mental Ability Scale
Let’s bring our Holzinger and Swineford Dataset back:
head(HolzingerSwineford1939)## id sex ageyr agemo school grade x1 x2 x3 x4 x5
## 1 1 1 13 1 Pasteur 7 3.333333 7.75 0.375 2.333333 5.75
## 2 2 2 13 7 Pasteur 7 5.333333 5.25 2.125 1.666667 3.00
## 3 3 2 13 1 Pasteur 7 4.500000 5.25 1.875 1.000000 1.75
## 4 4 1 13 2 Pasteur 7 5.333333 7.75 3.000 2.666667 4.50
## 5 5 2 12 2 Pasteur 7 4.833333 4.75 0.875 2.666667 4.00
## 6 6 2 14 1 Pasteur 7 5.333333 5.00 2.250 1.000000 3.00
## x6 x7 x8 x9
## 1 1.2857143 3.391304 5.75 6.361111
## 2 1.2857143 3.782609 6.25 7.916667
## 3 0.4285714 3.260870 3.90 4.416667
## 4 2.4285714 3.000000 5.30 4.861111
## 5 2.5714286 3.695652 6.30 5.916667
## 6 0.8571429 4.347826 6.65 7.500000?HolzingerSwineford1939This dataset has 301 cases with 9 mental ability items.
Assignment: Could you use the four models above to examine the dimensionality of this ODD Subscale?
Here is a factor structure that you may need:
cor.fac.HS.model = '
visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9
'Good luck!
bifac.model = '
# specific factors
visual =~ x2 + x3 # remove x1 because of heywood case
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9
# general factor GEN
G =~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9
'
bifac.model.fit = lavaan::sem(bifac.model,
data=HolzingerSwineford1939,
#ordered = colnames(odd),
std.lv = TRUE,
fixed.x = F,
orthogonal = TRUE,
estimator = 'MLR')
lavaan:::summary(bifac.model.fit, standardized = TRUE, fit.measures = TRUE)## lavaan 0.6-12 ended normally after 24 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 26
##
## Number of observations 301
##
## Model Test User Model:
## Standard Robust
## Test Statistic 36.711 36.204
## Degrees of freedom 19 19
## P-value (Chi-square) 0.009 0.010
## Scaling correction factor 1.014
## Yuan-Bentler correction (Mplus variant)
##
## Model Test Baseline Model:
##
## Test statistic 918.852 880.082
## Degrees of freedom 36 36
## P-value 0.000 0.000
## Scaling correction factor 1.044
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.980 0.980
## Tucker-Lewis Index (TLI) 0.962 0.961
##
## Robust Comparative Fit Index (CFI) 0.980
## Robust Tucker-Lewis Index (TLI) 0.962
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -3713.448 -3713.448
## Scaling correction factor 1.078
## for the MLR correction
## Loglikelihood unrestricted model (H1) -3695.092 -3695.092
## Scaling correction factor 1.051
## for the MLR correction
##
## Akaike (AIC) 7478.895 7478.895
## Bayesian (BIC) 7575.280 7575.280
## Sample-size adjusted Bayesian (BIC) 7492.823 7492.823
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.056 0.055
## 90 Percent confidence interval - lower 0.027 0.027
## 90 Percent confidence interval - upper 0.082 0.082
## P-value RMSEA <= 0.05 0.335 0.352
##
## Robust RMSEA 0.055
## 90 Percent confidence interval - lower 0.027
## 90 Percent confidence interval - upper 0.082
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.040 0.040
##
## Parameter Estimates:
##
## Standard errors Sandwich
## Information bread Observed
## Observed information based on Hessian
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv
## visual =~
## x2 0.751 0.366 2.050 0.040 0.751
## x3 0.223 0.007 30.882 0.000 0.223
## textual =~
## x4 0.854 0.067 12.802 0.000 0.854
## x5 1.035 0.063 16.494 0.000 1.035
## x6 0.782 0.057 13.746 0.000 0.782
## speed =~
## x7 0.717 0.084 8.510 0.000 0.717
## x8 0.701 0.081 8.710 0.000 0.701
## x9 0.441 0.057 7.688 0.000 0.441
## G =~
## x1 0.936 0.094 9.920 0.000 0.936
## x2 0.455 0.084 5.422 0.000 0.455
## x3 0.623 0.073 8.544 0.000 0.623
## x4 0.486 0.088 5.542 0.000 0.486
## x5 0.439 0.090 4.857 0.000 0.439
## x6 0.468 0.085 5.490 0.000 0.468
## x7 0.112 0.082 1.374 0.169 0.112
## x8 0.291 0.074 3.936 0.000 0.291
## x9 0.509 0.076 6.716 0.000 0.509
## Std.all
##
## 0.639
## 0.198
##
## 0.735
## 0.804
## 0.715
##
## 0.659
## 0.694
## 0.438
##
## 0.803
## 0.387
## 0.552
## 0.418
## 0.340
## 0.428
## 0.103
## 0.288
## 0.505
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv
## visual ~~
## textual 0.000 0.000
## speed 0.000 0.000
## G 0.000 0.000
## textual ~~
## speed 0.000 0.000
## G 0.000 0.000
## speed ~~
## G 0.000 0.000
## Std.all
##
## 0.000
## 0.000
## 0.000
##
## 0.000
## 0.000
##
## 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv
## .x2 0.612 0.513 1.191 0.234 0.612
## .x3 0.837 0.083 10.067 0.000 0.837
## .x4 0.384 0.051 7.598 0.000 0.384
## .x5 0.396 0.065 6.135 0.000 0.396
## .x6 0.366 0.046 7.933 0.000 0.366
## .x7 0.657 0.109 6.021 0.000 0.657
## .x8 0.446 0.095 4.687 0.000 0.446
## .x9 0.561 0.064 8.741 0.000 0.561
## .x1 0.482 0.152 3.178 0.001 0.482
## visual 1.000 1.000
## textual 1.000 1.000
## speed 1.000 1.000
## G 1.000 1.000
## Std.all
## 0.443
## 0.656
## 0.284
## 0.238
## 0.306
## 0.555
## 0.436
## 0.553
## 0.355
## 1.000
## 1.000
## 1.000
## 1.000