Chapter 5 PSM Matching Strategy

library(Matching)
library(MatchIt)
library(optmatch)
library(weights)
library(cem)
library(tcltk2)
library(knitr)
library(CBPS)
library(jtools)
library(cobalt)
library(lmtest)
library(sandwich) #vcovCL
library(rbounds) #gamma

5.1 Data

#data(lalonde)
lalonde = MatchIt::lalonde
dim(lalonde)
## [1] 614   9
names(lalonde)
## [1] "treat"    "age"      "educ"     "race"     "married"  "nodegree" "re74"     "re75"    
## [9] "re78"

5.1.1 Create dummy variable for race and unemployment

lalonde$black = ifelse(lalonde$race=='black', 1, 0)
lalonde$hispan = ifelse(lalonde$race=='hispan', 1, 0)
lalonde$un74 = ifelse(lalonde$re74==0, 1, 0)
lalonde$un75 = ifelse(lalonde$re75==0, 1, 0)

5.2 Regression Estimates

5.2.1 naive t-test estimate

reglm <- lm(re78 ~ treat, data = lalonde)
summ(reglm)
## MODEL INFO:
## Observations: 614
## Dependent Variable: re78
## Type: OLS linear regression 
## 
## MODEL FIT:
## F(1,612) = 0.93, p = 0.33
## R² = 0.00
## Adj. R² = -0.00 
## 
## Standard errors: OLS
## ----------------------------------------------------
##                        Est.     S.E.   t val.      p
## ----------------- --------- -------- -------- ------
## (Intercept)         6984.17   360.71    19.36   0.00
## treat               -635.03   657.14    -0.97   0.33
## ----------------------------------------------------

5.2.2 regression with covariates

reglm1 <- lm(re78 ~ treat + educ + age + black + hispan + married + nodegree + un74 + un75 + re74 + re75, data = lalonde)
summ(reglm1)
## MODEL INFO:
## Observations: 614
## Dependent Variable: re78
## Type: OLS linear regression 
## 
## MODEL FIT:
## F(11,602) = 10.75, p = 0.00
## R² = 0.16
## Adj. R² = 0.15 
## 
## Standard errors: OLS
## ------------------------------------------------------
##                         Est.      S.E.   t val.      p
## ----------------- ---------- --------- -------- ------
## (Intercept)          -137.00   2422.92    -0.06   0.95
## treat                 865.59    800.01     1.08   0.28
## educ                  349.38    158.47     2.20   0.03
## age                    -3.81     32.82    -0.12   0.91
## black               -1466.72    768.90    -1.91   0.06
## hispan                471.11    934.51     0.50   0.61
## married               445.25    690.83     0.64   0.52
## nodegree                3.18    845.33     0.00   1.00
## un74                 2492.95    807.49     3.09   0.00
## un75                  315.32    758.16     0.42   0.68
## re74                    0.38      0.06     6.05   0.00
## re75                    0.31      0.12     2.69   0.01
## ------------------------------------------------------

5.3 PSM Steps

5.3.1 Selection of covariates in X

fm1 = treat ~ age + educ + black + hispan + married + I(re74/1000) + I(re75/1000)
fm2 = treat ~ age + I(age^2) + I(age^3) + educ + black + hispan + married + I(re74/1000) + I(re75/1000)
fm3 = treat ~ age + I(age^2) + I(age^3) + educ + I(educ^2) + black + hispan + married + I(re74/1000) + I(re75/1000)

5.3.2 Calculation of propensity scores (p-scores)

pscore <- glm(fm2, data = lalonde, family = 'binomial')
head(pscore$fitted.values)
##      NSW1      NSW2      NSW3      NSW4      NSW5      NSW6 
## 0.5871794 0.3014102 0.9056376 0.9020139 0.9069395 0.8230760
hist(pscore$fitted.values[lalonde$treat==0],xlim=c(0,1))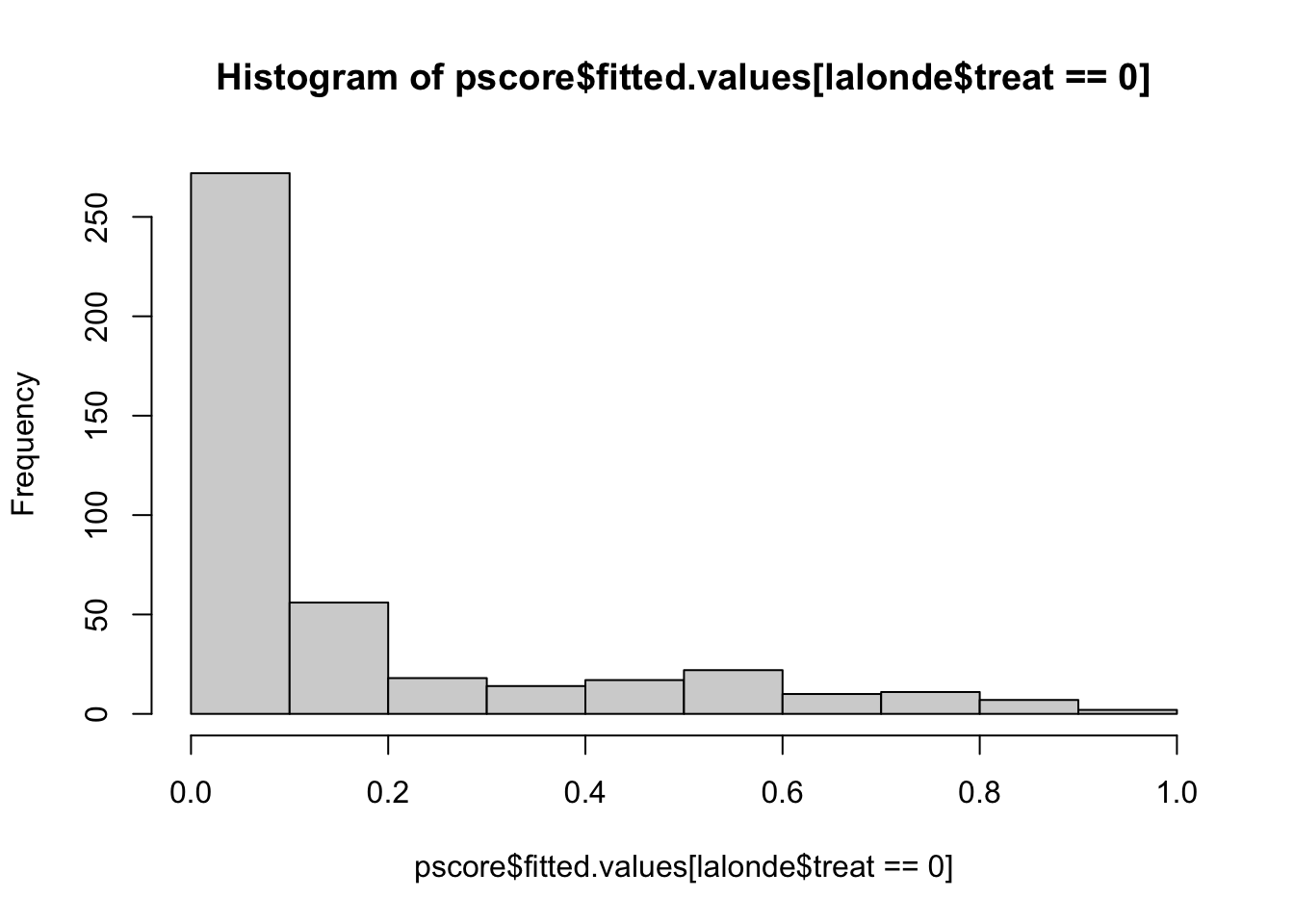

hist(pscore$fitted.values[lalonde$treat==1],xlim=c(0,1))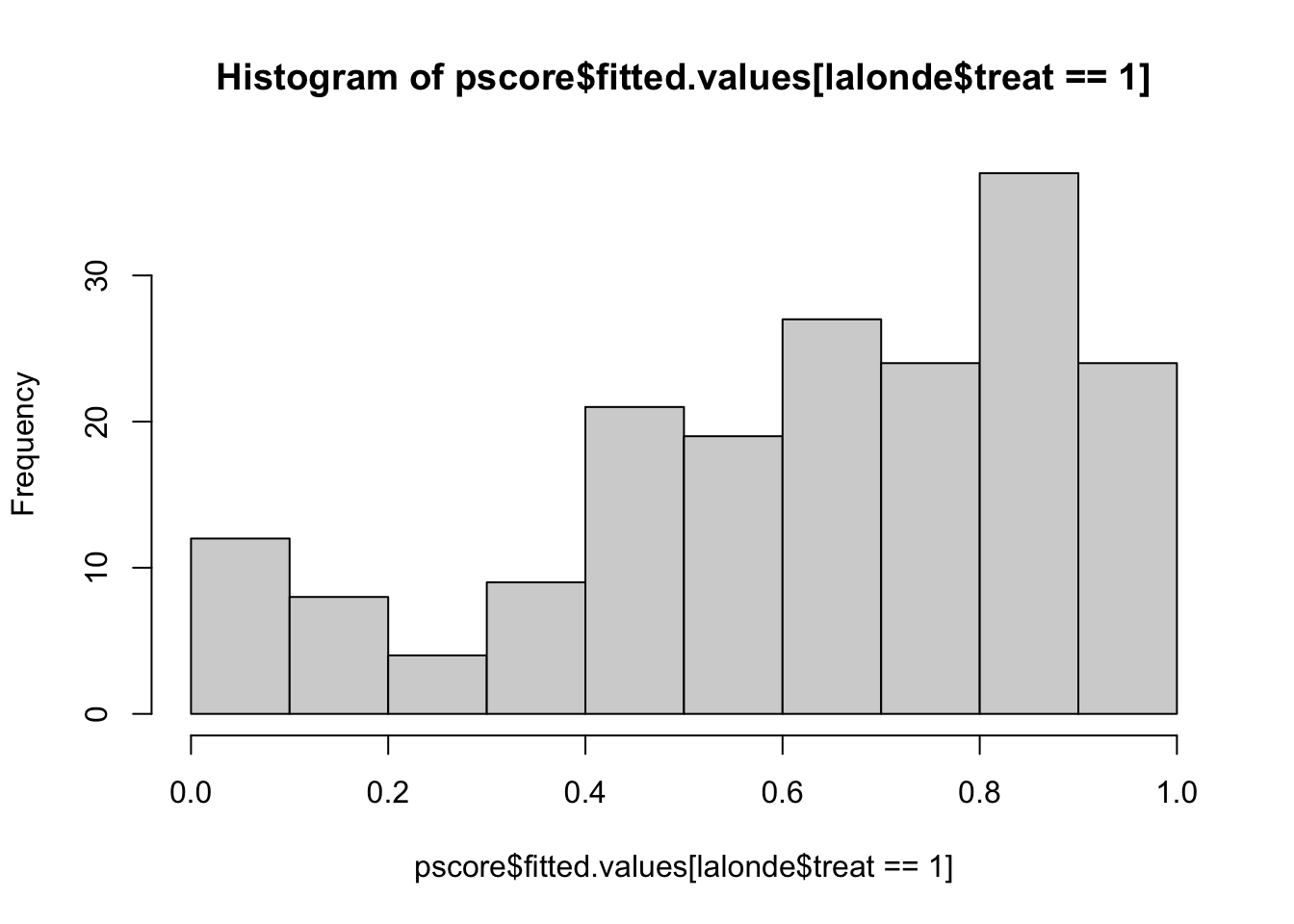

lalonde$pscore = pscore$fitted.values

Logistic regression:

summ(pscore)
## MODEL INFO:
## Observations: 614
## Dependent Variable: treat
## Type: Generalized linear model
##   Family: binomial 
##   Link function: logit 
## 
## MODEL FIT:
## χ²(9) = 310.83, p = 0.00
## Pseudo-R² (Cragg-Uhler) = 0.56
## Pseudo-R² (McFadden) = 0.41
## AIC = 460.66, BIC = 504.86 
## 
## Standard errors: MLE
## --------------------------------------------------
##                        Est.   S.E.   z val.      p
## ------------------ -------- ------ -------- ------
## (Intercept)          -18.92   4.22    -4.49   0.00
## age                    1.51   0.44     3.45   0.00
## I(age^2)              -0.04   0.01    -2.73   0.01
## I(age^3)               0.00   0.00     2.01   0.04
## educ                  -0.04   0.05    -0.76   0.45
## black                  3.06   0.30    10.17   0.00
## hispan                 0.68   0.45     1.51   0.13
## married               -1.34   0.31    -4.27   0.00
## I(re74/1000)          -0.10   0.03    -3.11   0.00
## I(re75/1000)           0.04   0.05     0.82   0.41
## --------------------------------------------------

try other formulas?

5.3.3 Matching based on p-sores

all in one function matchit():

set.seed(42)
m.out <- matchit(data = lalonde,
                 formula = fm1,
                 distance = "logit",
                 method = "nearest",
                 replace = TRUE,
                 caliper = 0.2, 
                 discard = 'both'
                 )

summary of matching results:

summary(m.out)
## 
## Call:
## matchit(formula = fm1, data = lalonde, method = "nearest", distance = "logit", 
##     discard = "both", replace = TRUE, caliper = 0.2)
## 
## Summary of Balance for All Data:
##              Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean eCDF Max
## distance            0.5722        0.1845          1.8020     0.8651    0.3763   0.6428
## age                25.8162       28.0303         -0.3094     0.4400    0.0813   0.1577
## educ               10.3459       10.2354          0.0550     0.4959    0.0347   0.1114
## black               0.8432        0.2028          1.7615          .    0.6404   0.6404
## hispan              0.0595        0.1422         -0.3498          .    0.0827   0.0827
## married             0.1892        0.5128         -0.8263          .    0.3236   0.3236
## I(re74/1000)        2.0956        5.6192         -0.7211     0.5181    0.2248   0.4470
## I(re75/1000)        1.5321        2.4665         -0.2903     0.9563    0.1342   0.2876
## 
## Summary of Balance for Matched Data:
##              Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean eCDF Max
## distance            0.5697        0.5692          0.0021     0.9848    0.0031   0.0546
## age                25.6885       25.5410          0.0206     0.4839    0.0728   0.2404
## educ               10.3224       10.6667         -0.1712     0.4586    0.0406   0.1475
## black               0.8415        0.8361          0.0150          .    0.0055   0.0055
## hispan              0.0601        0.0656         -0.0231          .    0.0055   0.0055
## married             0.1913        0.1858          0.0140          .    0.0055   0.0055
## I(re74/1000)        2.1185        2.3747         -0.0524     1.1054    0.0499   0.2896
## I(re75/1000)        1.5058        1.5431         -0.0116     1.3188    0.0397   0.1967
##              Std. Pair Dist.
## distance              0.0112
## age                   1.0654
## educ                  1.0083
## black                 0.0451
## hispan                0.2080
## married               0.3767
## I(re74/1000)          0.5800
## I(re75/1000)          0.7106
## 
## Sample Sizes:
##               Control Treated
## All            429.       185
## Matched (ESS)   42.44     183
## Matched         77.       183
## Unmatched      278.         0
## Discarded       74.         2
  • m.out$match.matrix
  • m.out$distance
  • plot(m.out\(distance, m.out\)fitted.values) # same
  • method: exact, subclass, optimal, full, cem
  • distance: pscore
  • plot(m.out, type = “qq”, interactive=FALSE)

5.3.4 Checking balance on covariates:

5.3.4.1 Balance for formula 1:

plot(summary(m.out))

5.3.4.2 Balance for formula 2:

set.seed(42)
m.out <- matchit(data = lalonde,
                 formula = fm2,
                 distance = "logit",
                 method = "nearest",
                 replace = TRUE,
                 caliper = 0.2, 
                 discard = 'both'
                 )
plot(summary(m.out))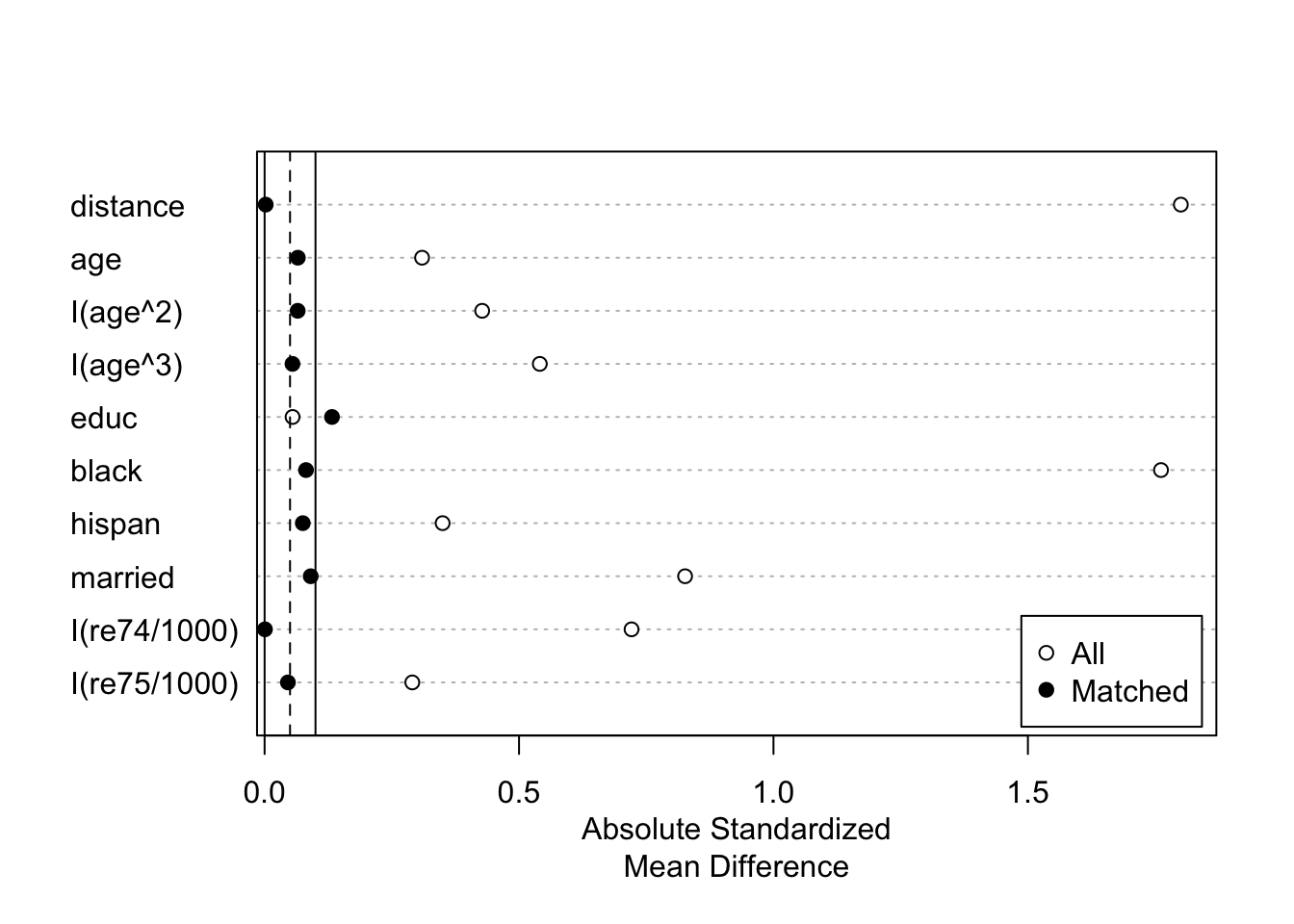

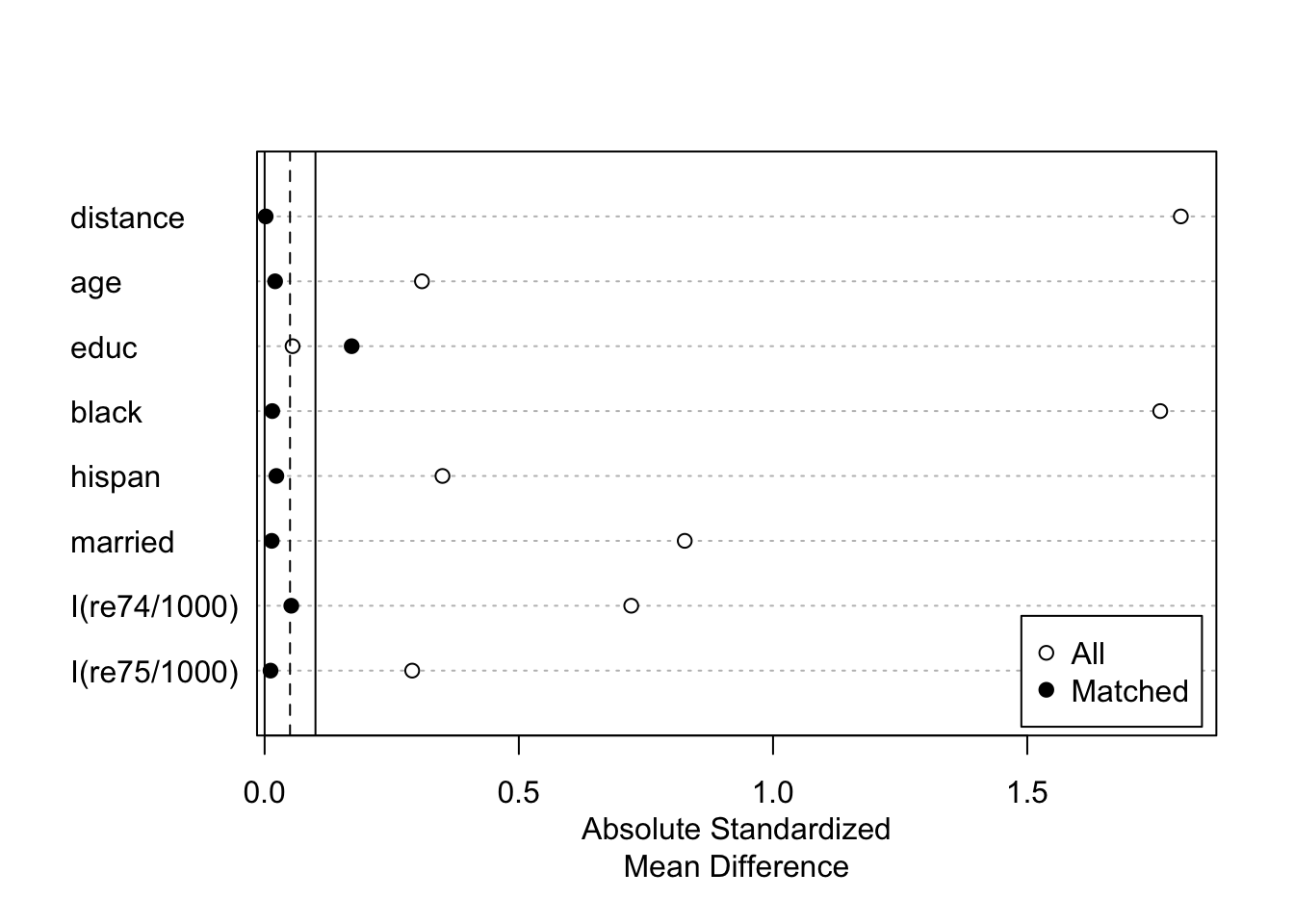
love.plot(m.out, binary = "std")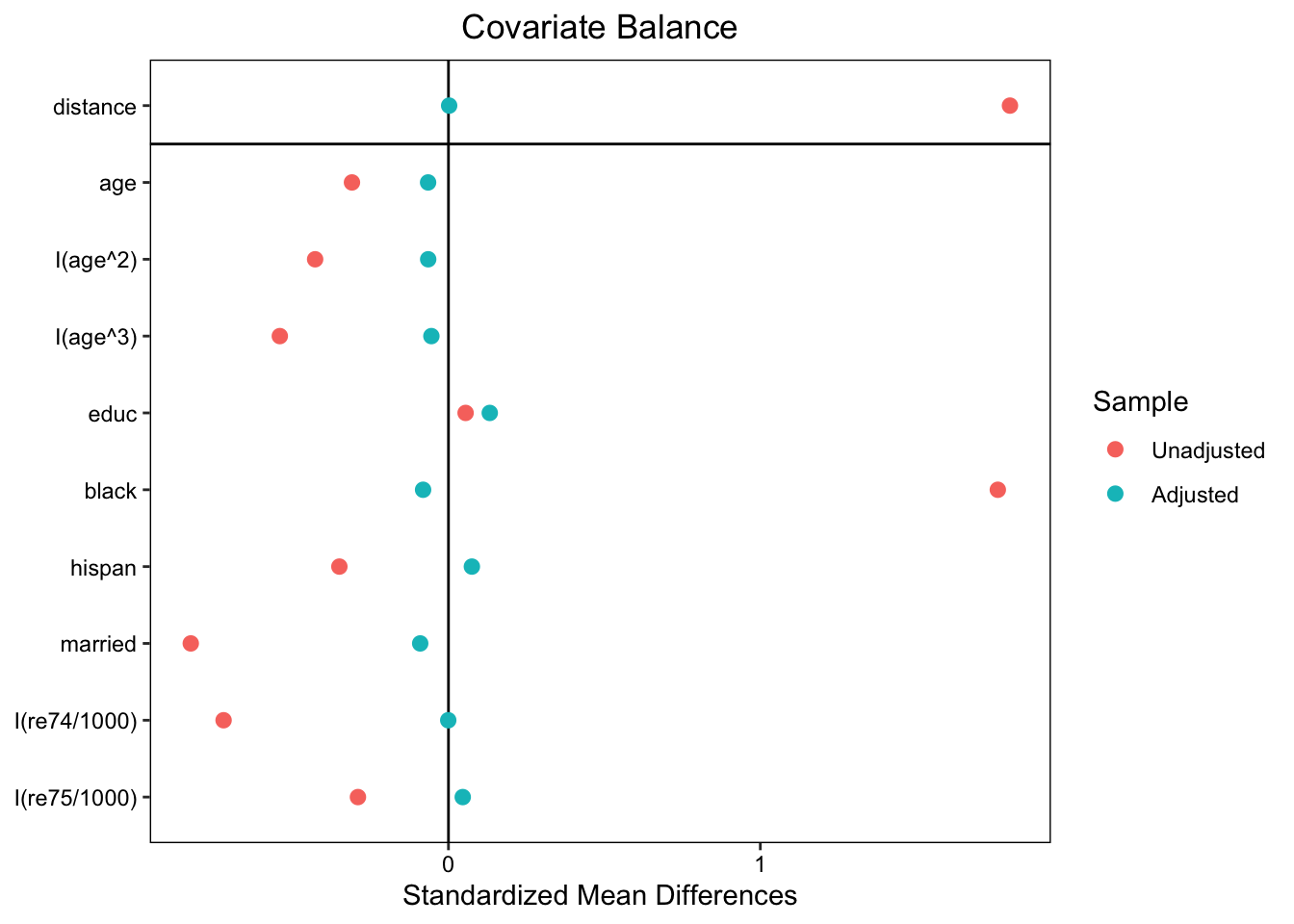

Standardized mean differences (SMD):

summary(m.out)
## 
## Call:
## matchit(formula = fm2, data = lalonde, method = "nearest", distance = "logit", 
##     discard = "both", replace = TRUE, caliper = 0.2)
## 
## Summary of Balance for All Data:
##              Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean eCDF Max
## distance            0.6237        0.1623          1.8005     1.3810    0.4018   0.6783
## age                25.8162       28.0303         -0.3094     0.4400    0.0813   0.1577
## I(age^2)          717.3946      901.7786         -0.4276     0.3627    0.0813   0.1577
## I(age^3)        21554.6595    32892.1142         -0.5408     0.2882    0.0813   0.1577
## educ               10.3459       10.2354          0.0550     0.4959    0.0347   0.1114
## black               0.8432        0.2028          1.7615          .    0.6404   0.6404
## hispan              0.0595        0.1422         -0.3498          .    0.0827   0.0827
## married             0.1892        0.5128         -0.8263          .    0.3236   0.3236
## I(re74/1000)        2.0956        5.6192         -0.7211     0.5181    0.2248   0.4470
## I(re75/1000)        1.5321        2.4665         -0.2903     0.9563    0.1342   0.2876
## 
## Summary of Balance for Matched Data:
##              Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean eCDF Max
## distance            0.5961        0.5956          0.0022     0.9866    0.0027   0.0533
## age                25.5089       25.9763         -0.0653     0.9175    0.0419   0.1361
## I(age^2)          705.0237      733.0651         -0.0650     0.9945    0.0419   0.1361
## I(age^3)        21242.4320    22390.9941         -0.0548     1.0300    0.0419   0.1361
## educ               10.4438       10.1775          0.1324     0.3762    0.0495   0.1834
## black               0.8284        0.8580         -0.0814          .    0.0296   0.0296
## hispan              0.0651        0.0473          0.0751          .    0.0178   0.0178
## married             0.2071        0.2426         -0.0906          .    0.0355   0.0355
## I(re74/1000)        2.2766        2.2802         -0.0007     1.2066    0.0364   0.2722
## I(re75/1000)        1.5084        1.3610          0.0458     1.7749    0.0272   0.1657
##              Std. Pair Dist.
## distance              0.0117
## age                   1.1503
## I(age^2)              1.0985
## I(age^3)              1.0232
## educ                  1.3037
## black                 0.1790
## hispan                0.3253
## married               0.6647
## I(re74/1000)          0.7456
## I(re75/1000)          0.6802
## 
## Sample Sizes:
##               Control Treated
## All            429.       185
## Matched (ESS)   47.21     169
## Matched         78.       169
## Unmatched      229.         0
## Discarded      122.        16
#out = summary(m.out)
#round(out$sum.all, 3)
#round(out$sum.matched, 3)
plot(m.out, type = "hist", interactive = F)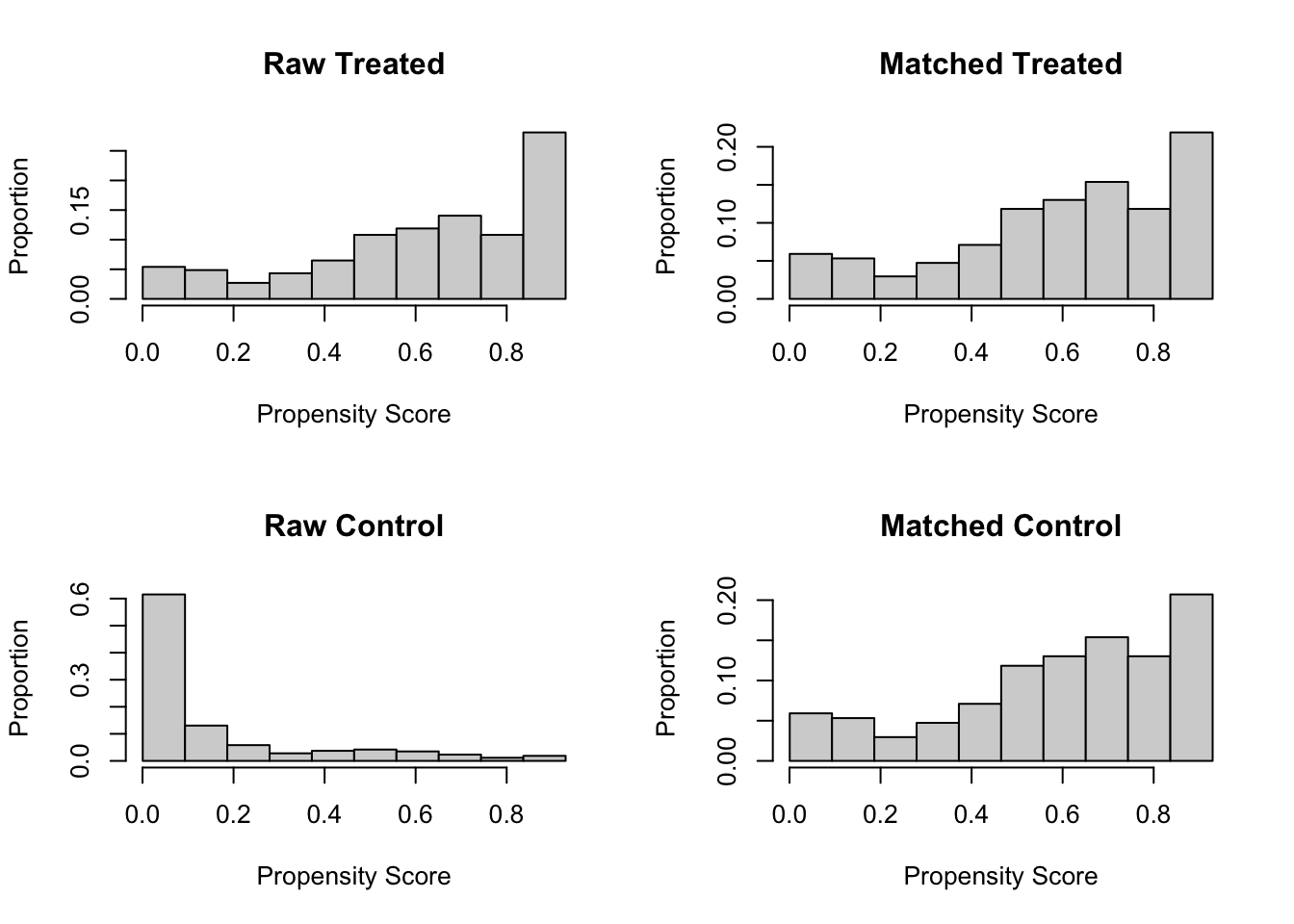

plot(m.out, type = "jitter", interactive = F)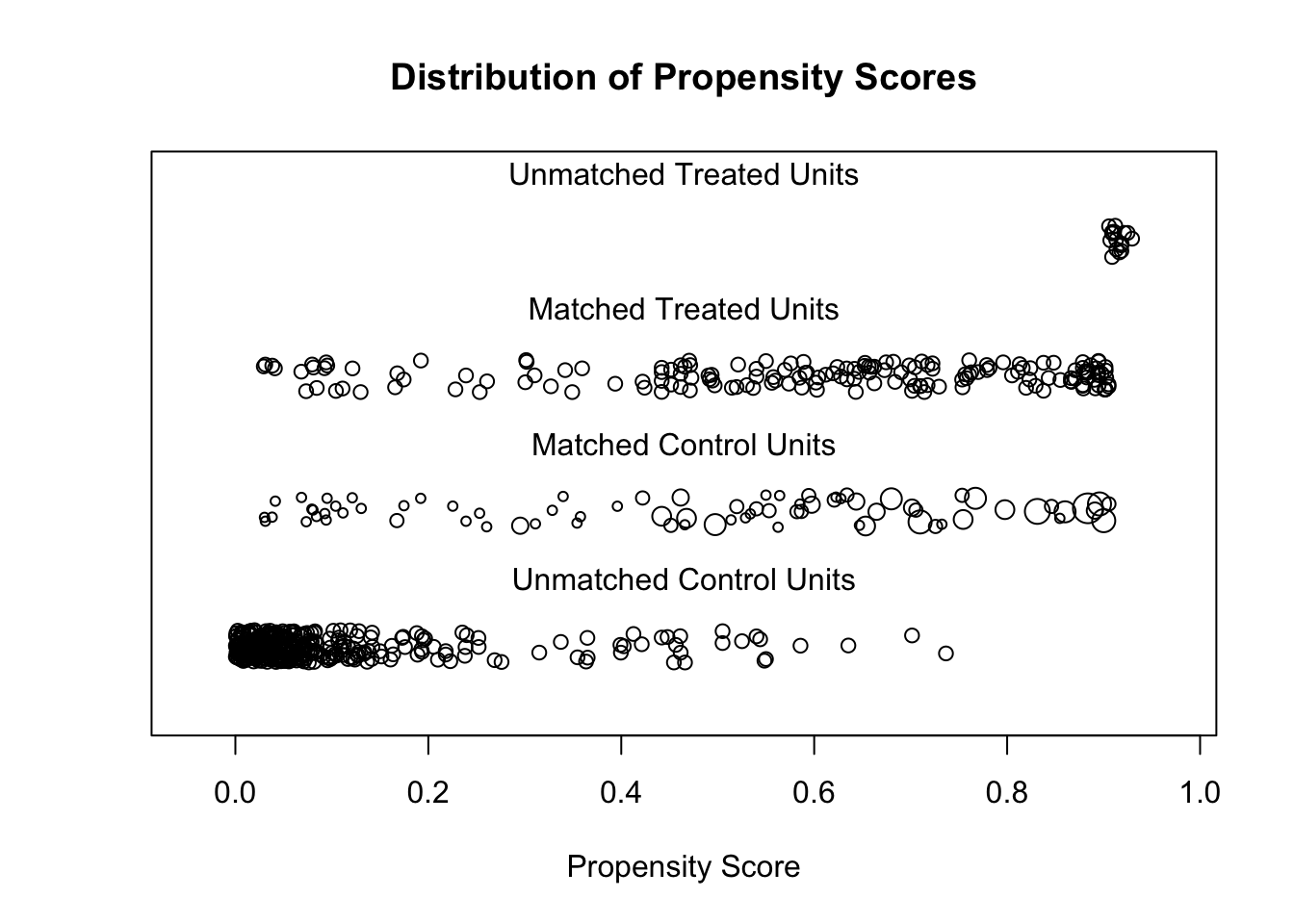

love.plot(m.out, binary = "std")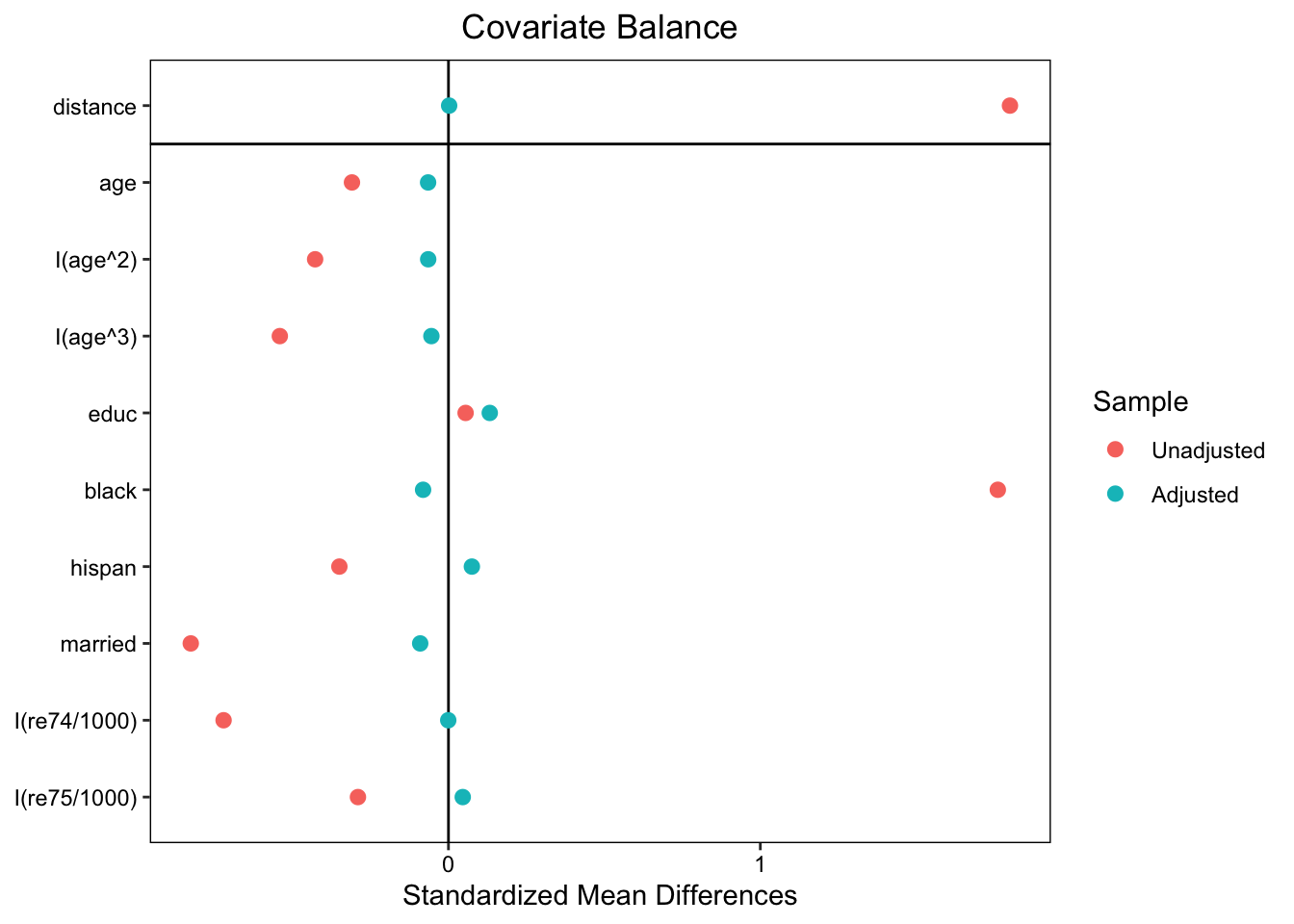

bal.plot(m.out, var.name = "distance", which = "both",
         type = "histogram", mirror = TRUE)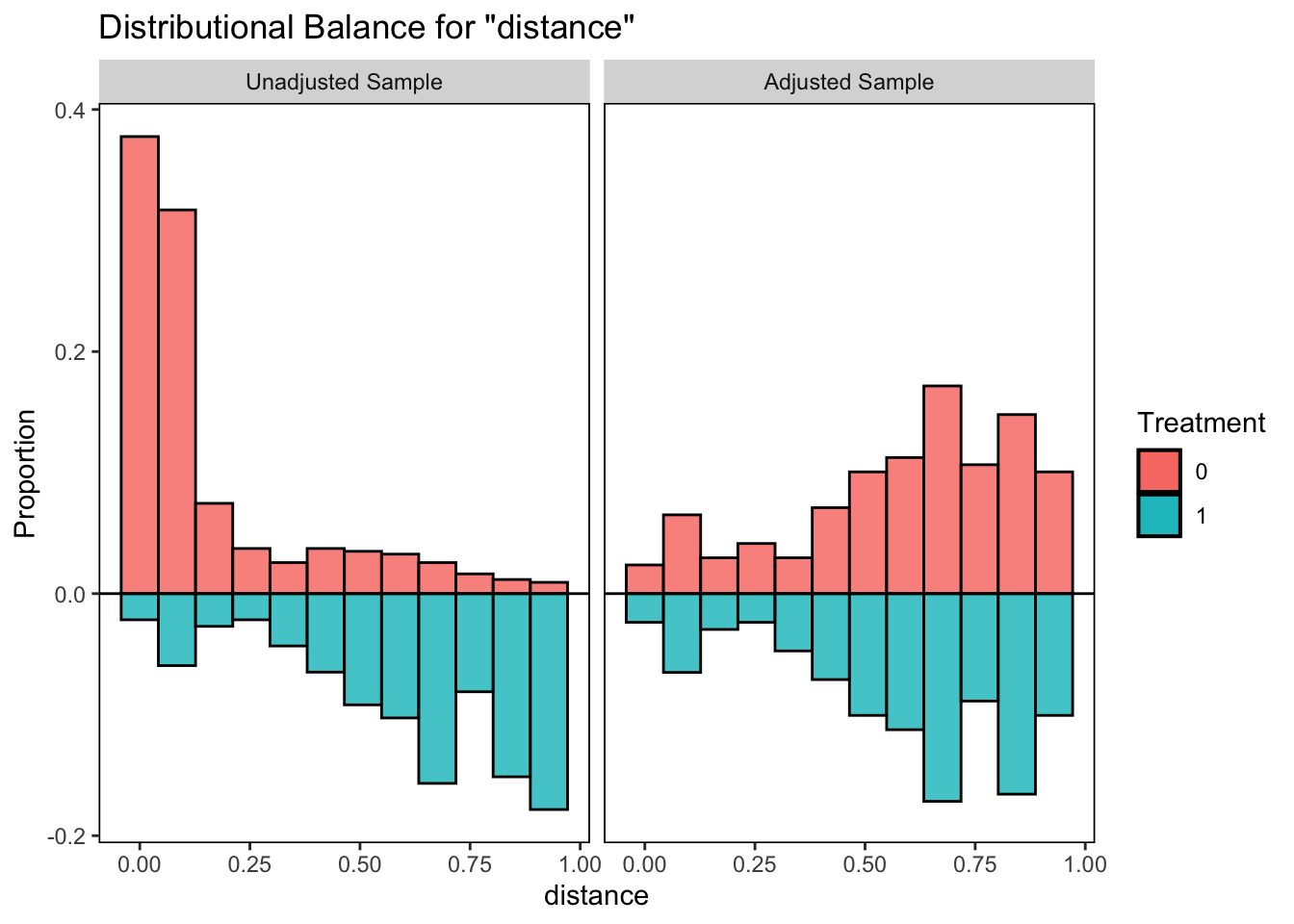

who matched to whom?

head(m.out$match.matrix, 10)
##       [,1]     
## NSW1  "PSID15" 
## NSW2  "PSID76" 
## NSW3  NA       
## NSW4  "PSID356"
## NSW5  NA       
## NSW6  "PSID269"
## NSW7  "PSID269"
## NSW8  "PSID356"
## NSW9  "PSID253"
## NSW10 "PSID329"

5.3.4.3 Balance for formula 3:

set.seed(42)
m.out <- matchit(data = lalonde,
                 formula = fm3,
                 distance = "logit",
                 method = "nearest",
                 replace = FALSE,
                 caliper = 0.2, 
                 discard = 'both'
                 )
summary(m.out)
## 
## Call:
## matchit(formula = fm3, data = lalonde, method = "nearest", distance = "logit", 
##     discard = "both", replace = FALSE, caliper = 0.2)
## 
## Summary of Balance for All Data:
##              Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean eCDF Max
## distance            0.6434        0.1538          1.8536     1.5312    0.4089   0.6923
## age                25.8162       28.0303         -0.3094     0.4400    0.0813   0.1577
## I(age^2)          717.3946      901.7786         -0.4276     0.3627    0.0813   0.1577
## I(age^3)        21554.6595    32892.1142         -0.5408     0.2882    0.0813   0.1577
## educ               10.3459       10.2354          0.0550     0.4959    0.0347   0.1114
## I(educ^2)         111.0595      112.8974         -0.0468     0.5173    0.0347   0.1114
## black               0.8432        0.2028          1.7615          .    0.6404   0.6404
## hispan              0.0595        0.1422         -0.3498          .    0.0827   0.0827
## married             0.1892        0.5128         -0.8263          .    0.3236   0.3236
## I(re74/1000)        2.0956        5.6192         -0.7211     0.5181    0.2248   0.4470
## I(re75/1000)        1.5321        2.4665         -0.2903     0.9563    0.1342   0.2876
## 
## Summary of Balance for Matched Data:
##              Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean eCDF Max
## distance            0.4892        0.4638          0.0961     1.1554    0.0146     0.10
## age                25.4100       24.7600          0.0908     0.9874    0.0238     0.09
## I(age^2)          713.2500      681.5000          0.0736     0.9455    0.0238     0.09
## I(age^3)        22175.6700    21050.3800          0.0537     0.8639    0.0238     0.09
## educ               10.2100       10.4000         -0.0945     0.9000    0.0163     0.09
## I(educ^2)         109.0500      113.5000         -0.1132     0.9644    0.0163     0.09
## black               0.7200        0.7300         -0.0275          .    0.0100     0.01
## hispan              0.1000        0.0800          0.0846          .    0.0200     0.02
## married             0.2500        0.2400          0.0255          .    0.0100     0.01
## I(re74/1000)        2.8664        3.0329         -0.0341     1.5574    0.0691     0.29
## I(re75/1000)        1.9818        2.1229         -0.0438     1.2273    0.0441     0.15
##              Std. Pair Dist.
## distance              0.0993
## age                   0.9602
## I(age^2)              0.9191
## I(age^3)              0.8759
## educ                  1.1190
## I(educ^2)             1.1640
## black                 0.4676
## hispan                0.7612
## married               0.7404
## I(re74/1000)          0.9759
## I(re75/1000)          1.0367
## 
## Sample Sizes:
##           Control Treated
## All           429     185
## Matched       100     100
## Unmatched     208      77
## Discarded     121       8
plot(summary(m.out))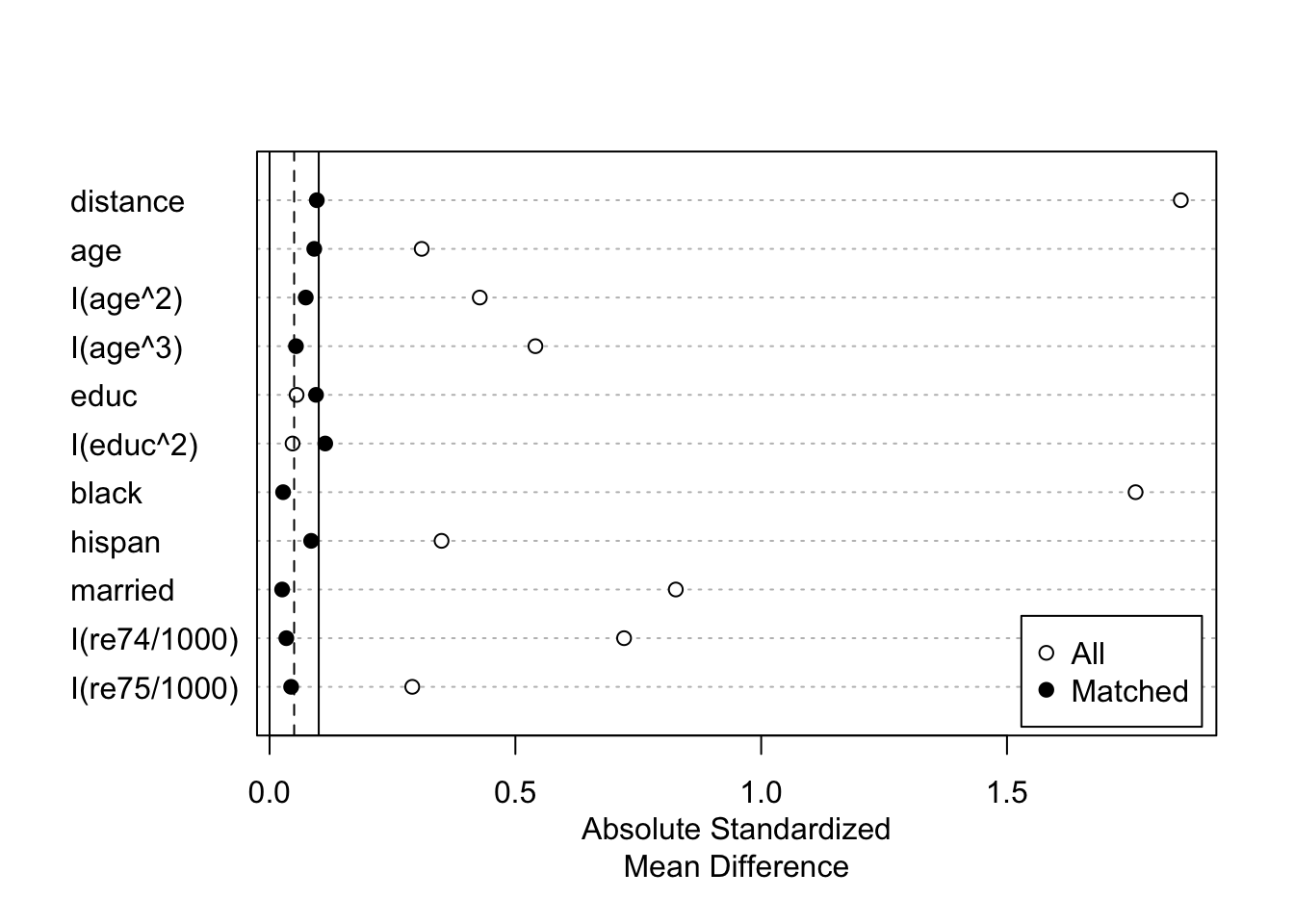

love.plot(m.out, binary = "std")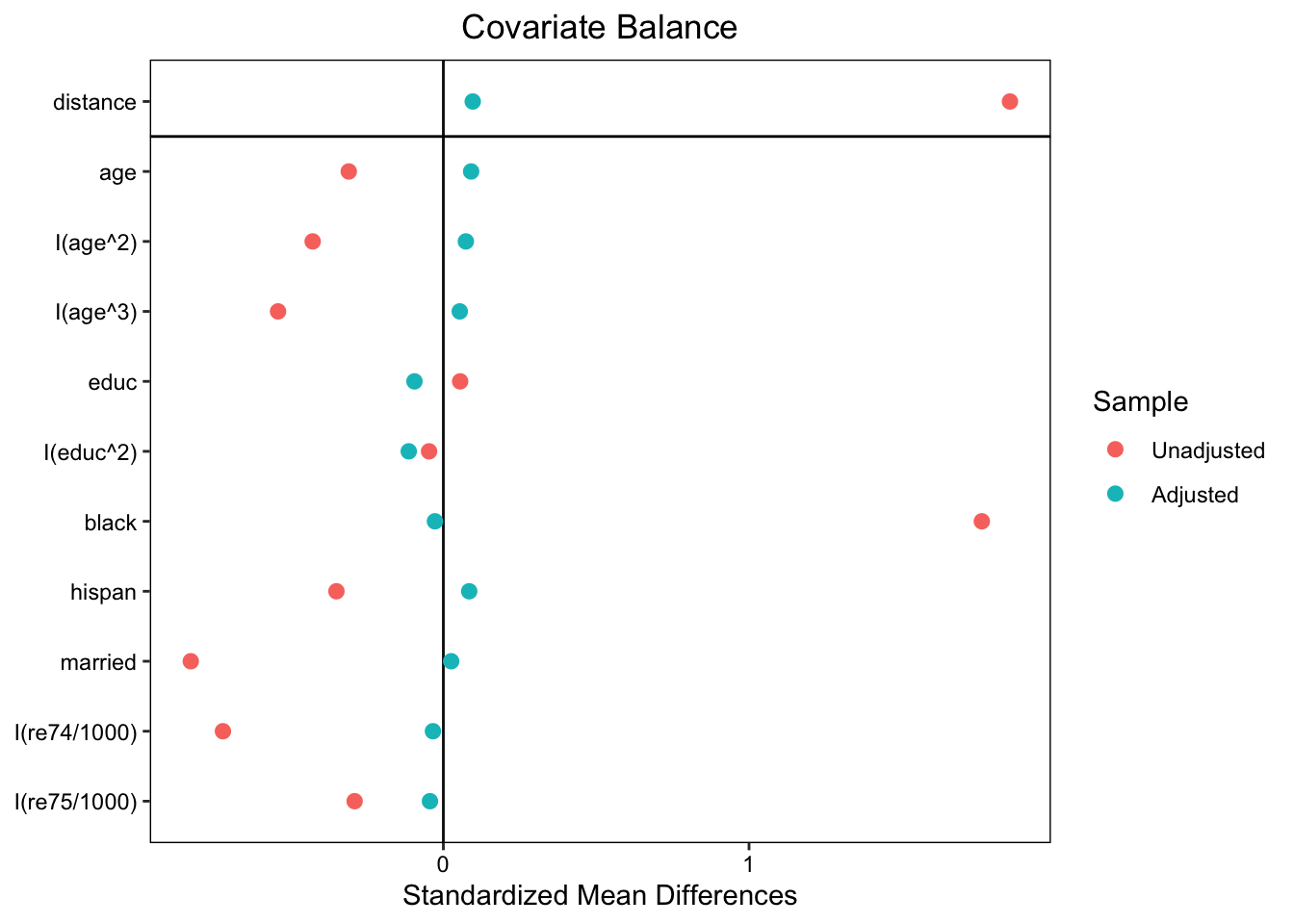

5.3.5 Estimation of treatment effect

I will use the matching results with fm3 because it yielded the best balance on the covariates between the matched groups. I also kept ratio = 1 and replace = FALSE to avoid the specification of weights for now:

set.seed(42)
m.out <- matchit(data = lalonde,
                 formula = fm3,
                 distance = "logit",
                 method = "nearest",
                 replace = FALSE,
                 ratio = 1, 
                 caliper = 0.2, 
                 discard = 'both',
                 estimand = 'ATC'
                 )
plot(summary(m.out))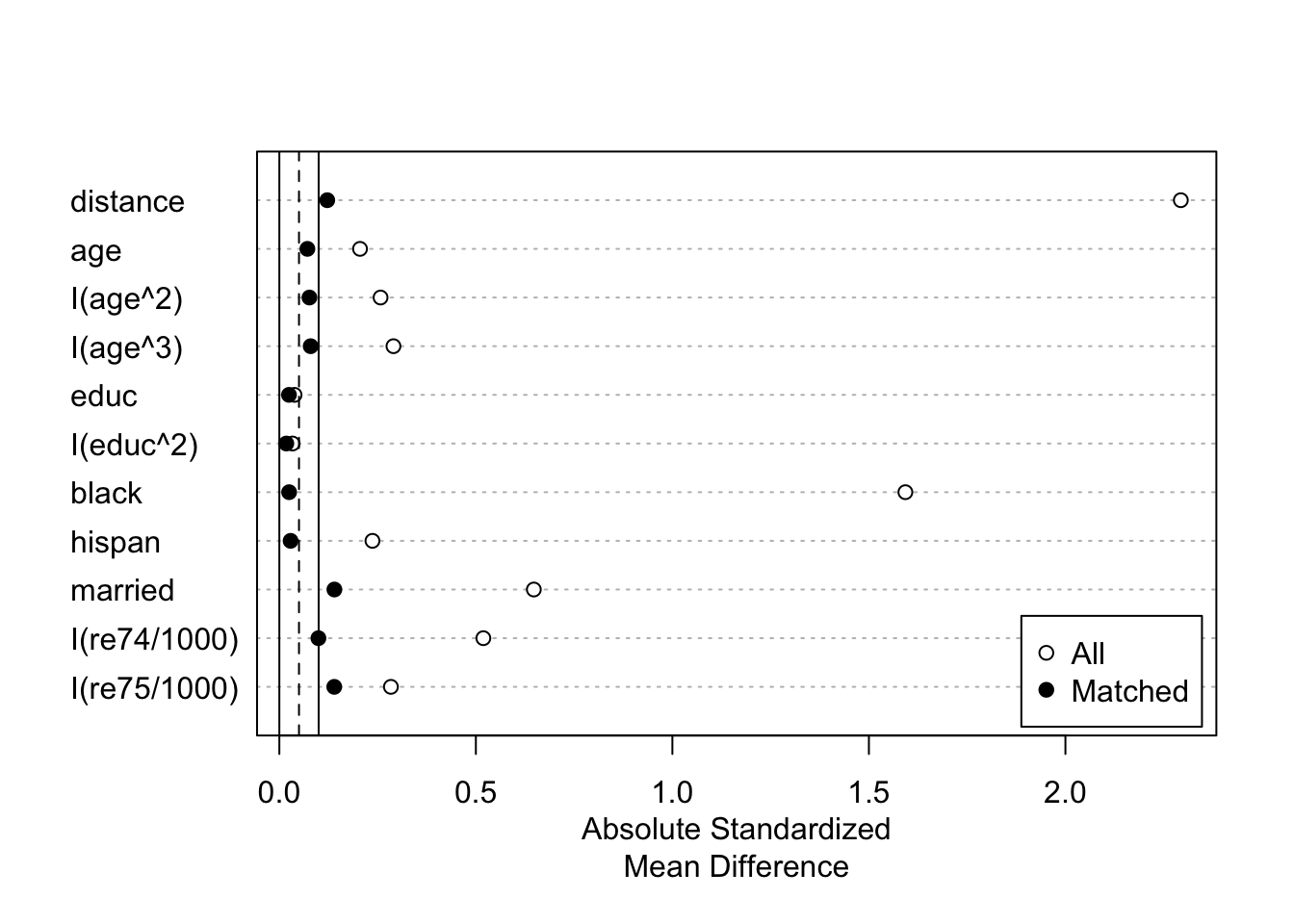

love.plot(m.out, binary = "std")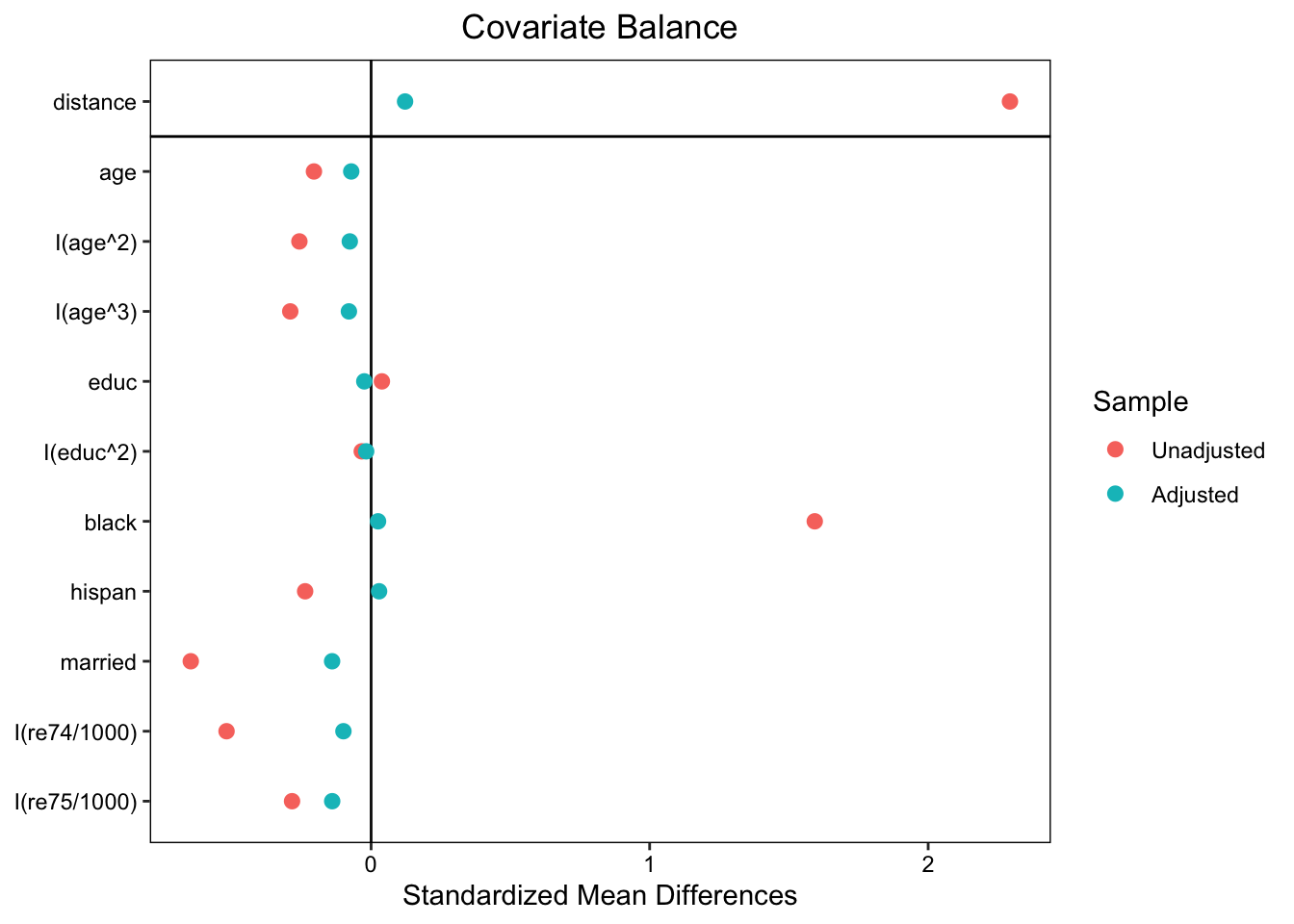

Extract matched data:

m.data <- match.data(m.out)
# m.data <- get_matches(m.out)
dim(m.data)
## [1] 200  17
head(m.data)
##       treat age educ   race married nodegree re74 re75      re78 black hispan un74 un75     pscore
## NSW2      1  22    9 hispan       0        1    0    0  3595.894     0      1    1    1 0.30141015
## NSW6      1  22    9  black       0        1    0    0  4056.494     1      0    1    1 0.82307603
## NSW9      1  22   16  black       0        0    0    0  2164.022     1      0    1    1 0.77887748
## NSW10     1  33   12  white       1        0    0    0 12418.070     0      0    1    1 0.09238612
## NSW12     1  21   13  black       0        0    0    0 17094.640     1      0    1    1 0.75335020
## NSW13     1  18    8  black       0        1    0    0     0.000     1      0    1    1 0.56957065
##        distance weights subclass
## NSW2  0.3896185       1       97
## NSW6  0.8771158       1       35
## NSW9  0.3024290       1       59
## NSW10 0.1029728       1       95
## NSW12 0.6782126       1       81
## NSW13 0.5923959       1       77

5.3.5.1 Linear model without covariates:

fit1 <- lm(re78 ~ treat, data = m.data)
summ(fit1)
## MODEL INFO:
## Observations: 200
## Dependent Variable: re78
## Type: OLS linear regression 
## 
## MODEL FIT:
## F(1,198) = 0.35, p = 0.55
## R² = 0.00
## Adj. R² = -0.00 
## 
## Standard errors: OLS
## ----------------------------------------------------
##                        Est.     S.E.   t val.      p
## ----------------- --------- -------- -------- ------
## (Intercept)         5665.91   665.62     8.51   0.00
## treat                557.46   941.33     0.59   0.55
## ----------------------------------------------------

Cluster-robust standard errors:

coeftest(fit1, vcov. = vcovCL)
## 
## t test of coefficients:
## 
##             Estimate Std. Error t value  Pr(>|t|)    
## (Intercept)  5665.91     661.58  8.5642 3.039e-15 ***
## treat         557.46     941.33  0.5922    0.5544    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

5.3.5.2 Weighted t-test

Alternatively, we use weighted Student’s t-test if ratio > 1 or replacement is allowed:

res <- wtd.t.test(m.data$re78[m.data$treat == 1],
                  m.data$re78[m.data$treat == 0],
                  weight = m.data$weights[m.data$treat == 1],
                  weighty = m.data$weights[m.data$treat == 0])
print(res)
## $test
## [1] "Two Sample Weighted T-Test (Welch)"
## 
## $coefficients
##     t.value          df     p.value 
##   0.5922000 197.9710298   0.5543924 
## 
## $additional
## Difference     Mean.x     Mean.y   Std. Err 
##   557.4575  6223.3714  5665.9139   941.3332
mu <- res$additional[1]
std <- res$additional[4]
cat("Confidence interval: ", sapply(qt(c(0.025, 0.975), coef(res)["df"]), function(x){return(mu+x*std)}), "\n")
## Confidence interval:  -1298.87 2413.785

5.3.5.3 Linear model with covariates: double robust (include just a few imbalanced covariates)

fit2 <- lm(re78 ~ treat + educ, data = m.data)
# include only the covariate that is not balanced
fit2 <- lm(re78 ~ treat + I(educ^2), data = m.data)
summ(fit2)
## MODEL INFO:
## Observations: 200
## Dependent Variable: re78
## Type: OLS linear regression 
## 
## MODEL FIT:
## F(2,197) = 5.54, p = 0.00
## R² = 0.05
## Adj. R² = 0.04 
## 
## Standard errors: OLS
## -----------------------------------------------------
##                        Est.      S.E.   t val.      p
## ----------------- --------- --------- -------- ------
## (Intercept)         1704.29   1374.35     1.24   0.22
## treat                591.81    919.14     0.64   0.52
## I(educ^2)             35.41     10.82     3.27   0.00
## -----------------------------------------------------
coeftest(fit2, vcov. = vcovCL)
## 
## t test of coefficients:
## 
##             Estimate Std. Error t value Pr(>|t|)   
## (Intercept) 1704.287   1452.586  1.1733 0.242101   
## treat        591.808    920.572  0.6429 0.521056   
## I(educ^2)     35.413     12.699  2.7886 0.005813 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

5.3.6 Hidden bias analysis

extract matched treatment and control units from m.data:

psens(x = m.data$re78[m.data$treat==1], 
      y = m.data$re78[m.data$treat==0], 
      Gamma = 3, GammaInc=0.1)
## 
##  Rosenbaum Sensitivity Test for Wilcoxon Signed Rank P-Value 
##  
## Unconfounded estimate ....  0.2508 
## 
##  Gamma Lower bound Upper bound
##    1.0      0.2508      0.2508
##    1.1      0.1409      0.3939
##    1.2      0.0739      0.5390
##    1.3      0.0366      0.6685
##    1.4      0.0173      0.7731
##    1.5      0.0079      0.8513
##    1.6      0.0035      0.9060
##    1.7      0.0015      0.9425
##    1.8      0.0006      0.9658
##    1.9      0.0003      0.9801
##    2.0      0.0001      0.9887
##    2.1      0.0000      0.9937
##    2.2      0.0000      0.9965
##    2.3      0.0000      0.9981
##    2.4      0.0000      0.9990
##    2.5      0.0000      0.9995
##    2.6      0.0000      0.9997
##    2.7      0.0000      0.9999
##    2.8      0.0000      0.9999
##    2.9      0.0000      1.0000
##    3.0      0.0000      1.0000
## 
##  Note: Gamma is Odds of Differential Assignment To
##  Treatment Due to Unobserved Factors 
##

a gamma value with 1.3 or larger could lead to a change in the ATT estimate.